Đồ thị của hàm sốĐồ thị của hàm số \(y = f(x)\) xác định trên tập D là tập hợp tất cả các điểm \(M(x;f(x))\) trên mặt phẳn tọa độ với mọi x thuộc D. Kí hiệu: \((C) = \{ M(x;f(x))|x \in D\} \) Quảng cáo
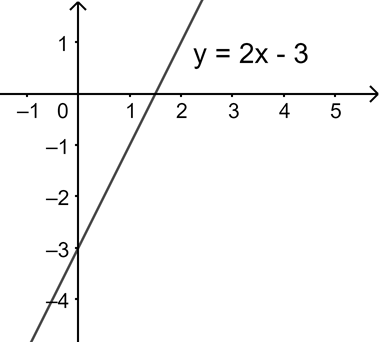
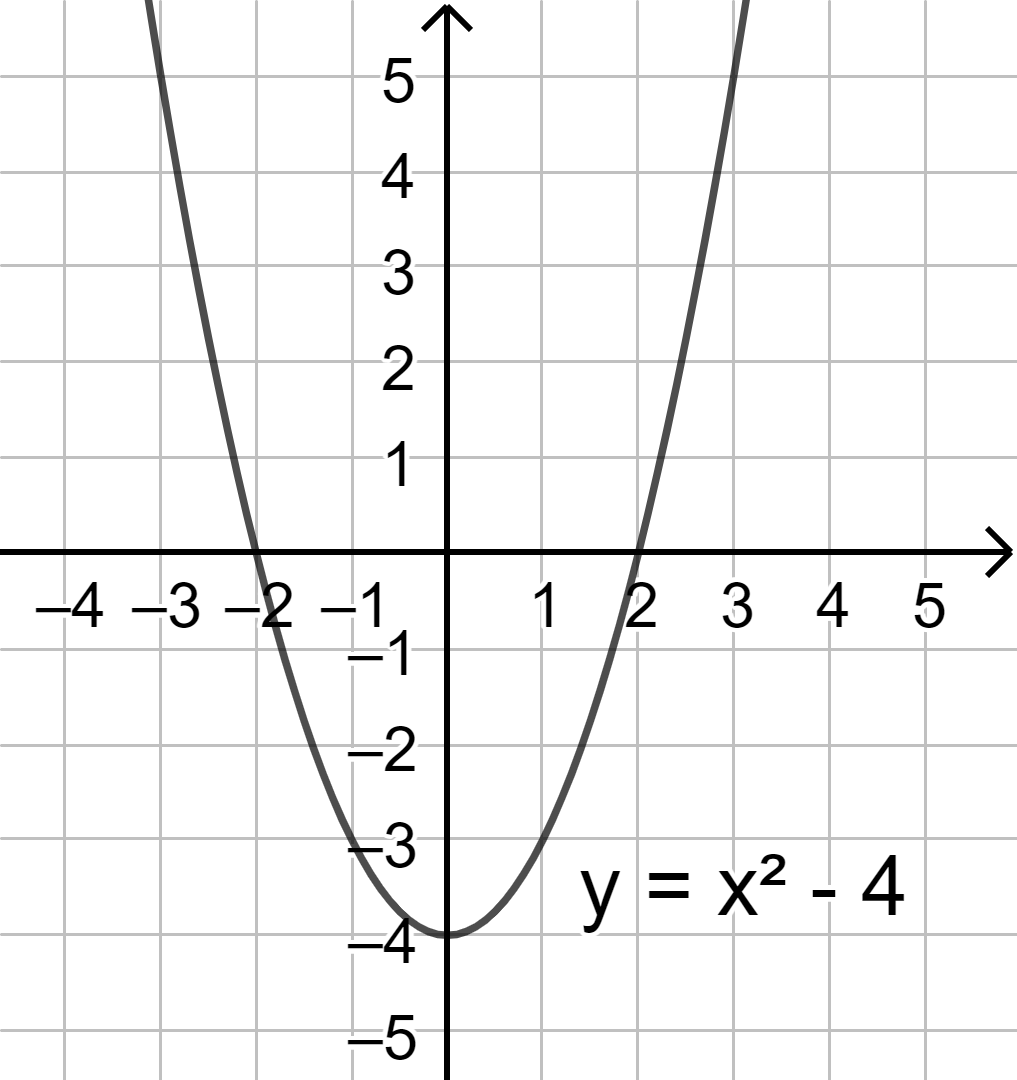
1. Lý thuyết + Định nghĩa: Đồ thị của hàm số \(y = f(x)\) xác định trên tập D là tập hợp tất cả các điểm \(M(x;f(x))\) trên mặt phẳn tọa độ với mọi x thuộc D. Kí hiệu: \((C) = \{ M(x;f(x))|x \in D\} \) + Kiểm tra điểm thuộc đồ thị hàm số Điểm \(M({x_M};{y_M})\) thuộc đồ thị hàm số \(y = f(x)\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_M} \in D\\{y_M} = f({x_M})\end{array} \right.\) Điểm \(M({x_M};{y_M})\) không thuộc đồ thị hàm số \(y = f(x)\)\( \Leftrightarrow \left[ \begin{array}{l}{x_M} \notin D\\{y_M} \ne f({x_M})\end{array} \right.\) 2. Ví dụ minh họa Đồ thị hàm số \(y = 2x - 3\) \((C) = \{ M(x;2x - 3)|x \in \mathbb{R}\} \) Đồ thị hàm số \(y = 2x - 3\) là đường thẳng, đi qua hai điểm (0;-3) và (1,5;0). Điểm thuộc đồ thị hàm số, điểm không thuộc đồ thị hàm số Quan sát đồ thị của hàm số \(y = {x^2} - 4\) Các điểm (2;0), (-2;0), (1; -3), (0;-4) thuộc đồ thị hàm số. Các điểm (2;2), (-2;3), (1; 2), (0;3) không thuộc đồ thị hàm số.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
