Nghiệm của bất phương trình bậc nhất hai ẩn. Biểu diễn miền nghiệm

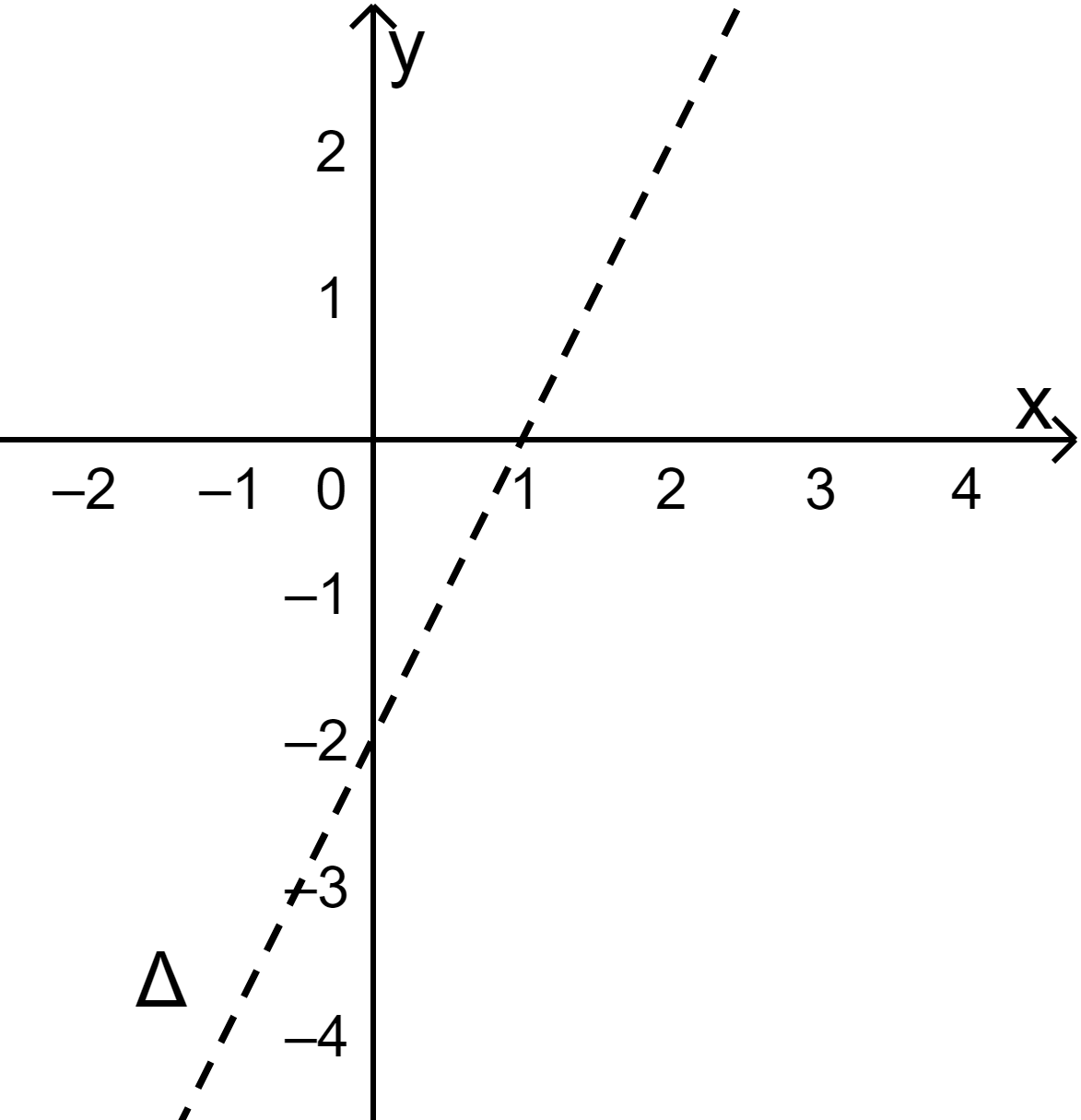
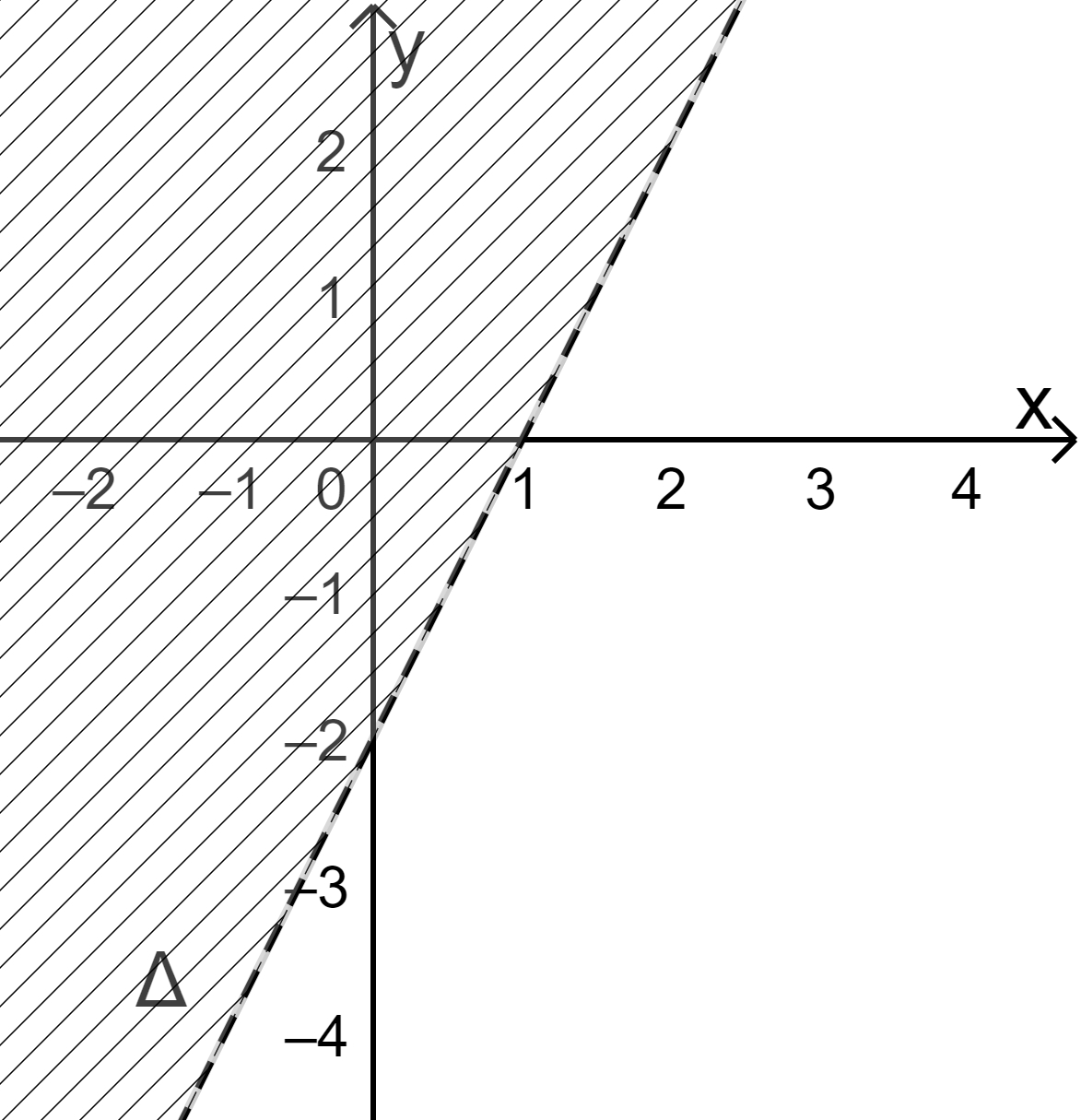
1. Lý thuyết

+ Định nghĩa:

Cặp số $({x_0};{y_0})$ thỏa mãn $a{x_0} + b{y_0} \le c$ được gọi là một nghiệm của bất phương trình $ax + by \le c$.

Nghiệm của các bất phương trình $ax + by < c;ax + by > c;ax + by \ge c$ được định nghĩa tương tự.

Trong mặt phẳng tọa độ $Oxy$, miền nghiệm của bất phương trình $ax + by \le c$ là tập hợp các điểm $({x_0};{y_0})$ sao cho $a{x_0} + b{y_0} \le c$.

+ Nhận xét

Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.

+ Biểu diễn miền nghiệm của bất phương trình $ax + by \le c$

Bước 1: Vẽ đường thẳng $\Delta :ax + by = c$

Bước 2: Lấy điểm $A({x_0};{y_0})$ không thuộc $\Delta$. Tính $a{x_0} + b{y_0}$ rồi so sánh với c.

Bước 3: Kết luận

Nếu $a{x_0} + b{y_0} < c$ thì miền nghiệm là nửa mặt phẳng (kể cả bờ $\Delta$) chứa điểm $A({x_0};{y_0})$.

Nếu $a{x_0} + b{y_0} > c$ thì miền nghiệm là nửa mặt phẳng (kể cả bờ $\Delta$) không chứa điểm $A({x_0};{y_0})$.

Chú ý: Đường thẳng $\Delta :ax + by = c$ là tập hợp các điểm (x;y) thỏa mãn $ax + by = c$.

Do đó miền nghiệm của các bất phương trình $ax + by < c;ax + by > c$ không chứa đường thẳng $\Delta$ (hay không kể bờ $\Delta$), khi đó ta thường vẽ $\Delta$ bằng nét đứt.

2. Ví dụ minh họa

+ Nghiệm của bất phương trình bậc nhất hai ẩn:

Cặp số $(2; - 1)$ là một nghiệm của bất phương trình $3x + 2y \ge  - 5$, vì  $3.2 + 2.( - 1) = 4 \ge  - 5$

Cặp số $( - 2;0)$ không là một nghiệm của bất phương trình $3x + 2y \ge  - 5$, vì  $3.( - 2) + 2.0 =  - 6 <  - 5$

+ Biểu diễn miền nghiệm của bất phương trình $2x - y > 2$

Bước 1: Vẽ đường thẳng $\Delta :2x - y = 2$ (nét đứt) đi qua (1;0) và (0; -2).

Bước 2: Lấy điểm $O(0;0)$ không thuộc $\Delta$. Ta có $2.0 - 0 = 0$ và $c = 2$.

Bước 3: Vì  $2.0 - 0 = 0 < 2$ nên điểm $O(0;0)$ không thuộc miền nghiệm.

Vậy miền nghiệm là nửa mặt phẳng (không kể bờ $\Delta$) không chứa điểm $O(0;0)$ (miền không gạch chéo).