Lý thuyết Trường hợp bằng nhau của tam giác vuông SGK Toán 7 - Kết nối tri thức

1. Ba trường hợp bằng nhau của tam giác vuông

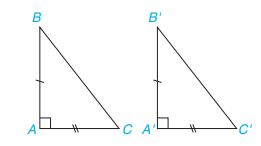
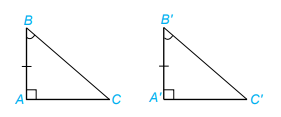
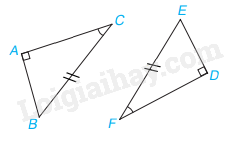
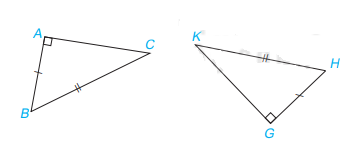
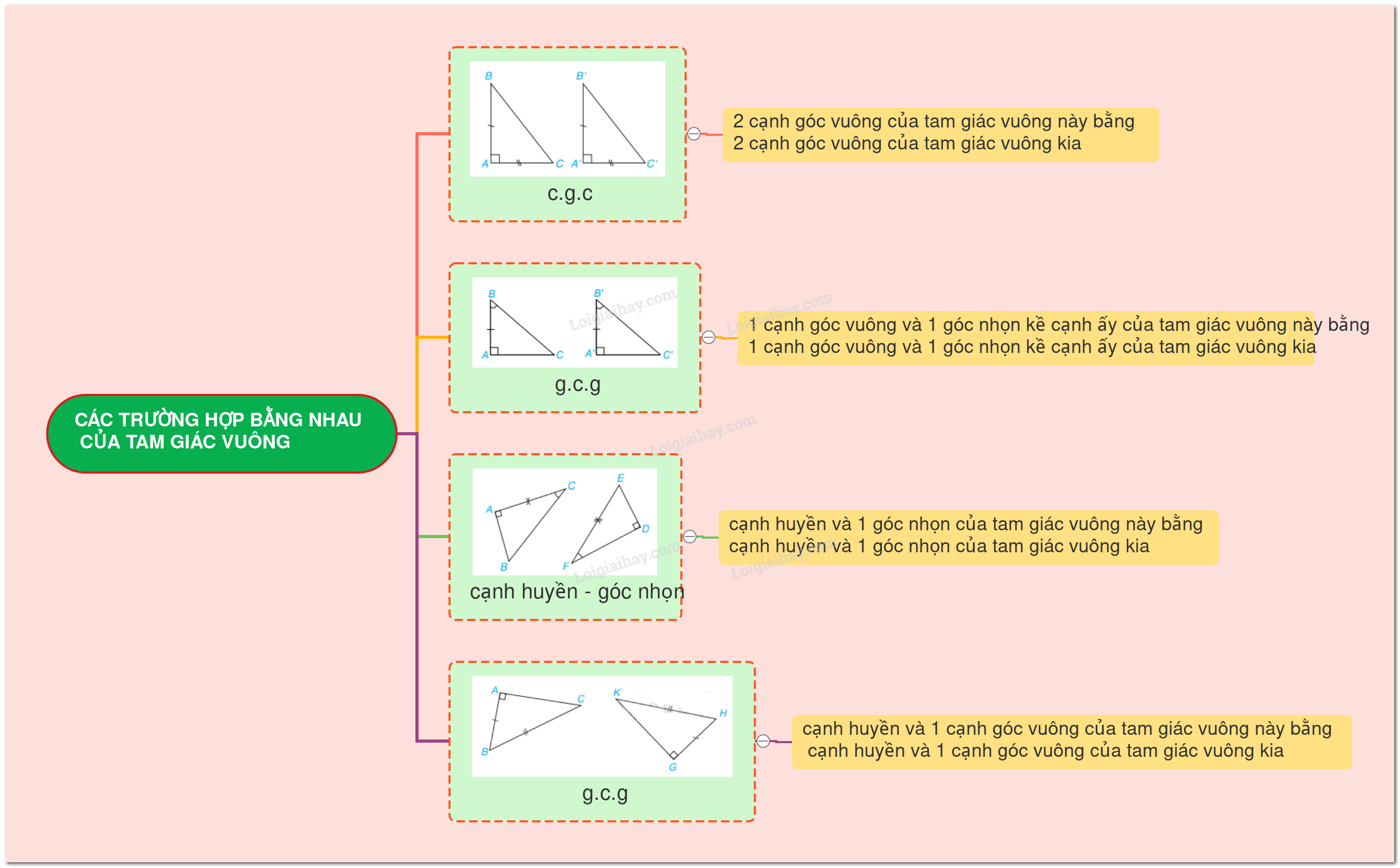
a) Nếu 2 cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. ( c.g.c)

Xét tam giác ABC và A’B’C’, ta có:

AB = A’B’

\(\widehat A = \widehat {A'}( = 90^\circ )\)

AC = A’C’

Vậy \(\Delta ABC = \Delta A'B'C'\) ( c.g.c)

b) Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. (g.c.g)

Xét tam giác ABC và A’B’C’, ta có:

\(\widehat A = \widehat {A'}( = 90^\circ )\)

AB = A’B’

\(\widehat B = \widehat {B'}\)

Vậy \(\Delta ABC = \Delta A'B'C'\) ( g.c.g)

c) Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. ( cạnh huyền – góc nhọn)

Xét tam giác vuông ABC và DEF, ta có:

AC = EF

\(\widehat C = \widehat F\)

Vậy \(\Delta ABC = \Delta DEF\) (cạnh huyền – góc nhọn)

2. Trường hợp bằng nhau đặc biệt của tam giác vuông

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau. ( cạnh huyền – cạnh góc vuông)

Xét tam giác vuông ABC và GHK, ta có:

BC = HK

AB = GH

Vậy \(\Delta ABC = \Delta GHK\) ( cạnh huyền – cạnh góc vuông)