Giải bài tập 5.30 trang 126 SGK Toán 9 tập 1 - Cùng khám phá

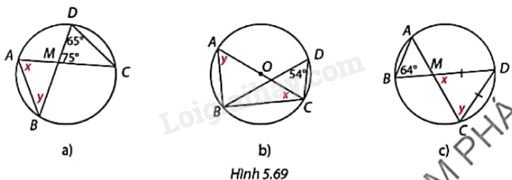
Đề bài

Tính các số đo x và y trong mỗi trường hợp ở Hình 5.69.

Lời giải chi tiết

a) \(\Delta \)MDC có: \(\widehat {BDC} + \widehat {DCM} + \widehat {DMC} = {180^o}\) nên

\(\widehat {DCM} = {180^o} - \widehat D - \widehat {DMC} = {180^o} - {65^o} - {75^o} = {40^o}\)

Vì góc CAB và góc BDC là góc ở nội tiếp cùng chắn cung BC nên \(x = \widehat {BDC} = {65^o}\).

Vì góc ACD và góc ABD là góc ở nội tiếp cùng chắn cung AD nên \(y = \widehat {ACD} = {40^o}\).

b) Vì góc BAC và góc BDC là góc ở nội tiếp cùng chắn cung BC nên \(y = \widehat {BDC} = {54^o}\) và số đo cung BC nhỏ là: \({2.54^o} = {108^o}\).

Số đo cung AB nhỏ là: \({180^o} - {108^o} = {72^o}\).

Vì góc ACB là góc ở nội tiếp chắn cung nhỏ AB nên \(x = \frac{1}{2}{.72^o} = {36^o}\).

c) Vì góc DBA và góc DCA là góc ở nội tiếp cùng chắn cung AD nên \(y = \widehat {ABD} = {64^o}\).

Tam giác MCD có: \(MD = CD\) nên tam giác MCD cân tại D. Do đó, \(x = y = {64^o}\).