Giải bài 7 trang 92 SGK Toán 10 tập 1 – Cánh diều

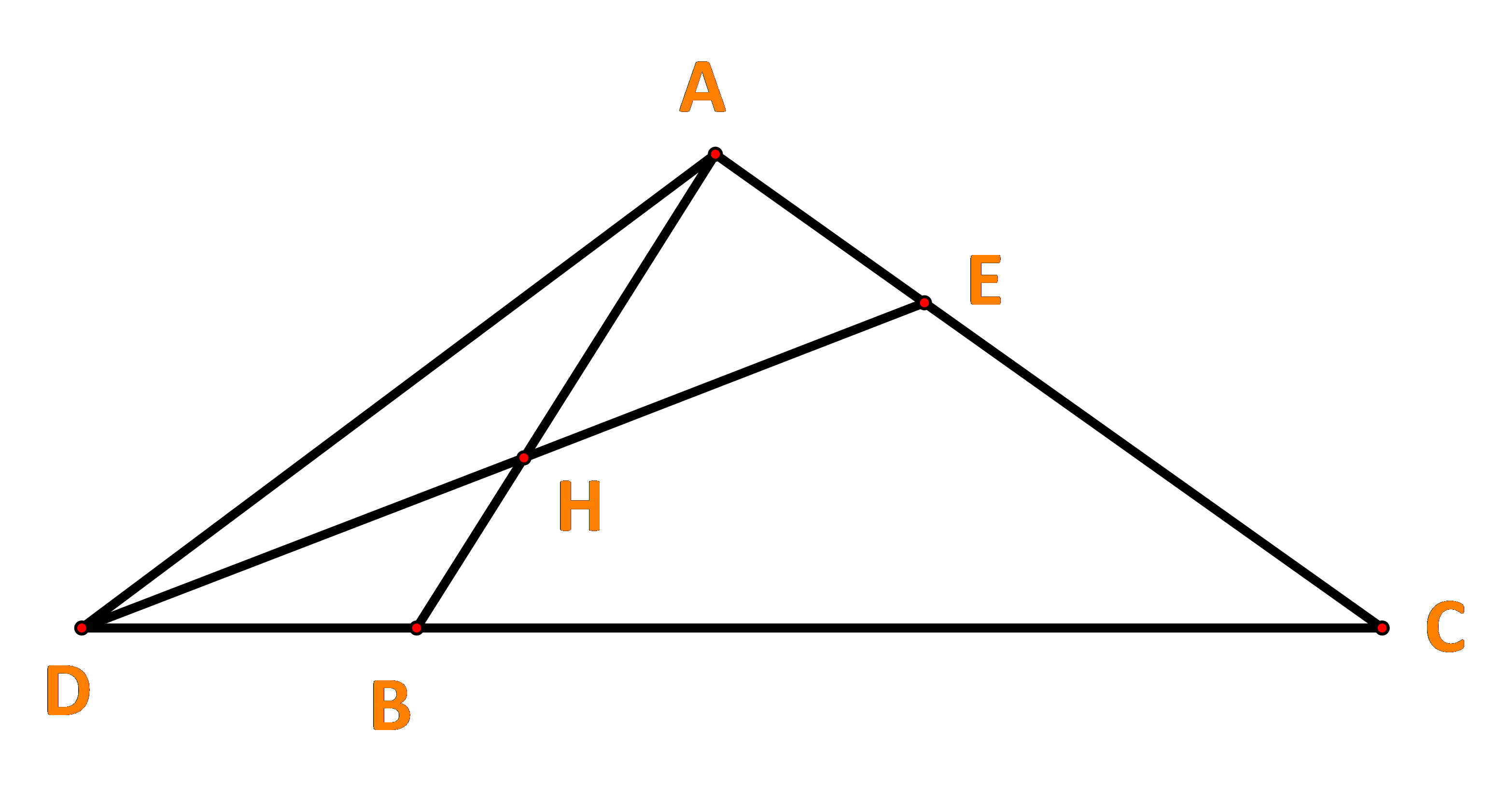
Đề bài

Cho tam giác ABC. Các điểm D, E, H thỏa mãn

\(\overrightarrow {DB}  = \frac{1}{3}\overrightarrow {BC} ,\;\overrightarrow {AE}  = \frac{1}{3}\overrightarrow {AC} ,\;\overrightarrow {AH}  = \frac{2}{3}\overrightarrow {AB} .\)

a) Biểu thị mỗi vecto \(\overrightarrow {AD} ,\overrightarrow {DH} ,\overrightarrow {HE} \) theo hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} .\)

b) Chứng minh D, E, H thẳng hàng.

Lời giải chi tiết

Dễ thấy: \(\overrightarrow {BC}  = \overrightarrow {BA}  + \overrightarrow {AC}  =  - \overrightarrow {AB}  + \overrightarrow {AC} \)

Ta có:

 +) \(\overrightarrow {AD}  = \overrightarrow {AB}  + \overrightarrow {BD} \). Mà \(\overrightarrow {BD}  =  - \overrightarrow {DB}  =  - \frac{1}{3}\overrightarrow {BC} \)

\( \Rightarrow \overrightarrow {AD}  = \overrightarrow {AB}  + \left( { - \frac{1}{3}} \right)( - \overrightarrow {AB}  + \overrightarrow {AC} ) = \frac{4}{3}\overrightarrow {AB}  - \frac{1}{3}\overrightarrow {AC} \)

+) \(\overrightarrow {DH}  = \overrightarrow {DA}  + \overrightarrow {AH}  =  - \overrightarrow {AD}  + \overrightarrow {AH} \).

Mà \(\overrightarrow {AD}  = \frac{4}{3}\overrightarrow {AB}  - \frac{1}{3}\overrightarrow {AC} ;\;\;\overrightarrow {AH}  = \frac{2}{3}\overrightarrow {AB} .\)

\( \Rightarrow \overrightarrow {DH}  =  - \left( {\frac{4}{3}\overrightarrow {AB}  - \frac{1}{3}\overrightarrow {AC} } \right) + \frac{2}{3}\overrightarrow {AB}  =  - \frac{2}{3}\overrightarrow {AB}  + \frac{1}{3}\overrightarrow {AC} .\)

+) \(\overrightarrow {HE}  = \overrightarrow {HA}  + \overrightarrow {AE}  =  - \overrightarrow {AH}  + \overrightarrow {AE} \)

Mà \(\overrightarrow {AH}  = \frac{2}{3}\overrightarrow {AB} ;\;\overrightarrow {AE}  = \frac{1}{3}\overrightarrow {AC} \)

\( \Rightarrow \overrightarrow {HE}  =  - \frac{2}{3}\overrightarrow {AB}  + \frac{1}{3}\overrightarrow {AC} .\)

b)

Theo câu a, ta có: \(\overrightarrow {DH}  = \overrightarrow {HE}  =  - \frac{2}{3}\overrightarrow {AB}  + \frac{1}{3}\overrightarrow {AC} \)

\( \Rightarrow \) Hai vecto \(\overrightarrow {DH} ,\overrightarrow {HE} \) cùng phương.

\( \Leftrightarrow \)D, E, H thẳng hàng