Giải bài 6 trang 105, 106 vở thực hành Toán 7 tập 2Cho hai đa thức (A = 6{x^3} - 4{x^2} - 12x - 7) và (B = 2{x^2} - 7). a) Xác định hệ số cao nhất và hệ số tự do trong mỗi đa thức đã cho. b) Tính giá trị của đa thức (A + B) tại (x = - 2). c) Chứng minh rằng (x = 0,x = - 1) và (x = 2) là ba nghiệm của đa thức (A - B). d) Trình bày phép nhân A.B bằng hai cách. e) Tìm đa thức R có bậc nhỏ hơn 2 sao cho hiệu (A - R) chia hết cho B. Quảng cáo
Đề bài Cho hai đa thức \(A = 6{x^3} - 4{x^2} - 12x - 7\) và \(B = 2{x^2} - 7\). a) Xác định hệ số cao nhất và hệ số tự do trong mỗi đa thức đã cho. b) Tính giá trị của đa thức \(A + B\) tại \(x = - 2\). c) Chứng minh rằng \(x = 0,x = - 1\) và \(x = 2\) là ba nghiệm của đa thức \(A - B\). d) Trình bày phép nhân A.B bằng hai cách. e) Tìm đa thức R có bậc nhỏ hơn 2 sao cho hiệu \(A - R\) chia hết cho B. Phương pháp giải - Xem chi tiết a) - Cho một đa thức. Khi đó: + Hệ số của hạng tử có bậc cao nhất gọi là hệ số cao nhất. + Hệ số của hạng tử bậc 0 (hạng tử không chứa biến) gọi là hệ số tự do. b, c) + Để cộng (trừ) hai đa thức, ta viết hai đa thức trong dấu ngoặc và nối chúng bởi dấu “+” (hay “\( - \)”). Sau đó bỏ dấu ngoặc rồi nhóm các hạng tử cùng bậc và thu gọn. + Nếu tại \(x = a\) (a là một số), giá trị của một đa thức bằng 0 thì ta gọi a (hay \(x = a\)) là một nghiệm của đa thức đó. + Để tính giá trị đa thức tại \(x = - 2\), ta thay \(x = - 2\) vào đa thức \(A + B\) vừa tính ở trên, rút gọn ta thu được kết quả. d) – Muốn một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau. – Sử dụng cách đặt tính nhân để thực hiện phép tính: + Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trong một dòng riêng. + Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau (để thực hiện phép cộng theo cột). e) + Thực hiện phép chia A cho B được thương là Q và số dư là R, ta viết biểu thức dưới dạng \(A = B.Q + R\), từ đó tìm được đa thức R. Lời giải chi tiết a) Hệ số cao nhất của \(A = 6{x^3} - 4{x^2} - 12x - 7\) là 6 và hệ số tự do là -7. Hệ số cao nhất của \(B = 2{x^2} - 7\) là 2 và hệ số tự do là -7. b) Đặt \(S\left( x \right) = A + B\), ta có \(S\left( x \right) = \left( {6{x^3} - 4{x^2} - 12x - 7} \right) + \left( {2{x^2} - 7} \right) = 6{x^3} - 2{x^2} - 12x - 14\) Giá trị của \(A + B\) tại \(x = - 2\) là: \(S\left( { - 2} \right) = 6.{\left( { - 2} \right)^3} - 2.{\left( { - 2} \right)^2} - 12.\left( { - 2} \right) - 14 = - 48 - 8 + 24 - 14 = - 46\) c) Đặt \(D\left( x \right) = A - B\), ta có \(D\left( x \right) = \left( {6{x^3} - 4{x^2} - 12x - 7} \right) - \left( {2{x^2} - 7} \right) = 6{x^3} - 6{x^2} - 12x\) Ta có: \(D\left( 0 \right) = 0;D\left( { - 1} \right) = 6.{\left( { - 1} \right)^3} - 6.{\left( { - 1} \right)^2} - 12.\left( { - 1} \right) = 0\) và \(D\left( 2 \right) = {6.2^3} - {6.2^2} - 12.2 = 0\). Vậy \(x = 0,x = - 1\), \(x = 2\) là các nghiệm của D(x). d) Cách 1: Khai triển tích: \(A.B = \left( {6{x^3} - 4{x^2} - 12x - 7} \right)\left( {2{x^2} - 7} \right)\) \( = 6{x^3}.2{x^2} - 4{x^2}.2{x^2} - 12x.2{x^2} - 7.2{x^2} - 7.6{x^3} + 7.4{x^2} + 7.12x + 7.7\) \( = 12{x^5} - 8{x^4} - 24{x^3} - 14{x^2} - 42{x^3} + 28{x^2} + 84x + 49\) \( = 12{x^5} - 8{x^4} - 66{x^3} + 14{x^2} + 84x + 49\) Cách 2: Đặt tính nhân:
e) Chia A cho B bằng cách đặt tính chia:
Từ đó suy ra: \(6{x^3} - 4{x^2} - 12x - 7 = \left( {2{x^2} - 7} \right)\left( {3x - 2} \right) + \left( {9x - 21} \right)\) Nếu đặt \(R = 9x - 21\) thì đẳng thức trên có nghĩa là \(A = B.\left( {3x - 2} \right) + R\), suy ra \(A - R = B\left( {3x - 2} \right)\) Vậy \(A - R\) chia hết cho B và đa thức cần tìm là \(R = 9x - 21\).
|














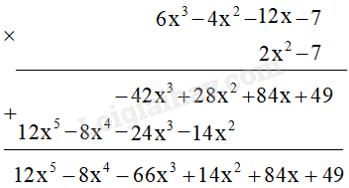
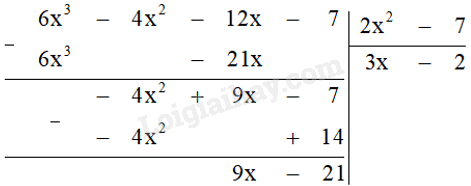






Danh sách bình luận