Bài 53 trang 166 SBT toán 8 tập 1

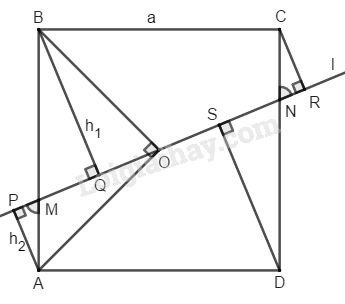
Đề bài

Qua tâm \(O\) của hình vuông \(ABCD\) cạnh \(a,\) kẻ đường thẳng \(l\) cắt cạnh \(AB\) và \(CD\) lần lượt tại \(M\) và \(N.\) Biết \(MN = b.\) Hãy tính tổng các khoảng cách từ các đỉnh của hình vuông đến đường thẳng \(l\) theo \(a\) và \(b\) (\(a\) và \(b\) có cùng đơn vị đo)

Lời giải chi tiết

Gọi \(h_1\) và \(h_2\)  là khoảng cách từ đỉnh \(B\) và đỉnh \(A\) đến đường thẳng \(l\); gọi tổng khoảng cách là \(S.\)

Vì \(O\) là tâm đối xứng của hình vuông.

\(⇒ OM = ON,OA=OC\) (tính chất đối xứng tâm)

Suy ra: \(AM = CN\) (đối xứng qua \(O\))

\(\widehat {AMP} = \widehat {DNS}\) (đồng vị)

\(\widehat {DNS} = \widehat {CNR}\) (đối đỉnh)

\( \Rightarrow \widehat {AMP} = \widehat {CNR}\)

Suy ra: \(∆ APM = ∆ CRN\) (cạnh huyền, góc nhọn)

\(⇒ CR = AP =h_2\) 

\(AM = CN\) (hai cạnh tương ứng)

\(⇒ BM = DN\)

\(\widehat {BMQ} = \widehat {DNS}\) (so le trong)

Suy ra: \(∆ BQM = ∆ DSN\) (cạnh huyền, góc nhọn) \(⇒ DS = BQ =h_1\)

\(\eqalign{  & {S_{BOA}} = {1 \over 4}{S_{ABCD}} = {1 \over 4}{a^2}\,(1) }\) 

\(\eqalign{{S_{BOA}} = {S_{BOM}} + {S_{AOM}} }\)

\(\eqalign{= {1 \over 2}{b \over 2}.{h_1} + {1 \over 2}{b \over 2}.{h_2} }\) 

\(\eqalign{= {b \over 4}\left( {{h_1} + {h_2}} \right)\,(2) }\)

Từ \((1)\) và \((2):\) \({h_1} + {h_2} = \dfrac{{{a^2}}}{b}\)

\(S = 2\left( {{h_1} + {h_2}} \right) = \dfrac{{2{a^2}} }{ b}\)

Loigiaihay.com