Bài 4 trang 83 SBT toán 8 tập 2

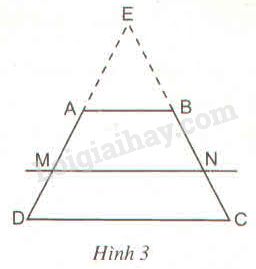
Đề bài

Cho hình thang \(ABCD\) có \(AB // CD\) và \(AB < CD\).

Đường thẳng song song với đáy \(AB\) cắt các cạnh bên \(AD, BC\) theo thứ tự tại \(M\) và \(N.\)

Chứng minh rằng:

a. \(\displaystyle{{MA} \over {AD}} = {{NB} \over {BC}}\)

b. \(\displaystyle{{MA} \over {MD}} = {{NB} \over {NC}}\)

c. \(\displaystyle{{MD} \over {DA}} = {{NC} \over {CB}}\)

HD: Kéo dài các tia \(DA, CB\) cắt nhau tại \(E\) (h.3), áp dụng định lí Ta-lét trong tam giác và tính chất của tỉ lệ thức để chứng minh.

Lời giải chi tiết

a) Gọi \(E\) là giao điểm của \(AD\) và \(BC.\)

Xét \(∆ EMN\) có \(AB // MN\) (gt)

Theo định lí Ta-lét ta có:

\(\displaystyle{{EA} \over {MA}} = {{EB} \over {NB}}\)

\(\Rightarrow \displaystyle{{EA} \over {EB}} = {{MA} \over {NB}}\)  (1)

Xét \(∆ EDC\) có \(AB // CD\) (gt)

Theo định lí Ta-lét ta có:

\(\displaystyle{{EA} \over {AD}} = {{EB} \over {BC}}\)

\(\Rightarrow \displaystyle{{EA} \over {EB}} = {{AD} \over {BC}}\) (2)

Từ (1) và (2) suy ra: \(\displaystyle {{MA} \over {NB}} = {{AD} \over {BC}}\)

\(\displaystyle \Rightarrow {{MA} \over {AD}} = {{NB} \over {BC}}\)

b) Ta có \(\displaystyle{{MA} \over {AD}} = {{NB} \over {BC}}\) (câu a)

Suy ra:

\(\displaystyle{{MA} \over {AD - MA}} = {{NB} \over {BC - NB}}\)

\(\displaystyle \Rightarrow {{MA} \over {MD}} = {{NB} \over {NC}}\)

c) Ta có \(\displaystyle{{MA} \over {MD}} = {{NB} \over {NC}}\) (câu b)

\( \Rightarrow \dfrac{{MD}}{{MA}} = \dfrac{{NC}}{{NB}}\)

Suy ra:

\(\displaystyle {{MD} \over {MA + MD}} = {{NC} \over {NB + NC}} \)

\(\displaystyle \Rightarrow {{MD} \over {DA}} = {{NC} \over {CB}}\)

Loigiaihay.com