Giải bài 3 trang 24 SGK Toán 10 tập 1 – Cánh diều

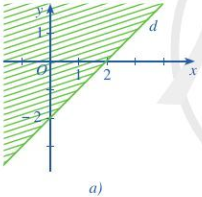
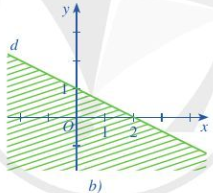
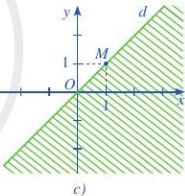
Đề bài

Nửa mặt phẳng không bị gạch (không kể đường thẳng d) ở mỗi Hình 7a, 7b, 7c là miền nghiệm của bất phương trình nào?

Lời giải chi tiết

 a) Giả sử đường thẳng d có dạng y = ax + b

Vì đường thẳng d qua điểm (2;0) và (0;-2) nên ta có:

\(\left\{ \begin{array}{l}0 = 2a + b\\ - 2 = b\end{array} \right.\)

Suy ra, b = -2 và a = 1, tức y = x - 2

Vậy phương trình đường thẳng là \(x-y-2=0\)

Lấy điểm (3;0) thuộc miền nghiệm ta có 3-0-2=1>0

=> Bất phương trình cần tìm là \(x - y - 2 > 0\)

b) Đường thẳng qua điểm (2;0) và (0;1)

Thay x=2, y=0 vào phương trình \(y = ax + b\) ta được \(0 = 2a + b\)

Thay x=0, y=1 vào phương trình \(y = ax + b\) ta được \(1 = 0.a + b\)

=> \(a =  - \frac{1}{2},b = 1\)

=> phương trình đường thẳng là \(y =  - \frac{1}{2}x + 1\)

Lấy điểm (3;0) thuộc miền nghiệm ta có \( - \frac{1}{2}x + 1 - y = \frac{{ - 1}}{2} < 0\)

=> Bất phương trình cần tìm là \( - \frac{1}{2}x - y + 1 < 0\)

c) Đường thẳng qua điểm (0;0) và (1;1)

Thay x=0, y=0 vào phương trình \(y = ax + b\) ta được \(b=0\)

Thay x=1, y=1 vào phương trình \(y = ax + b\) ta được \(1 = a + b\)

Suy ra, a = 1, b = 0, tức y = x

Vậy phương trình đường thẳng là x-y=0

Lấy điểm (0;1) thuộc miền nghiệm ta có x-y=-1<0

=> Bất phương trình cần tìm là \(x - y < 0\)