Giải bài 2 trang 24 SGK Toán 10 tập 1 – Cánh diều

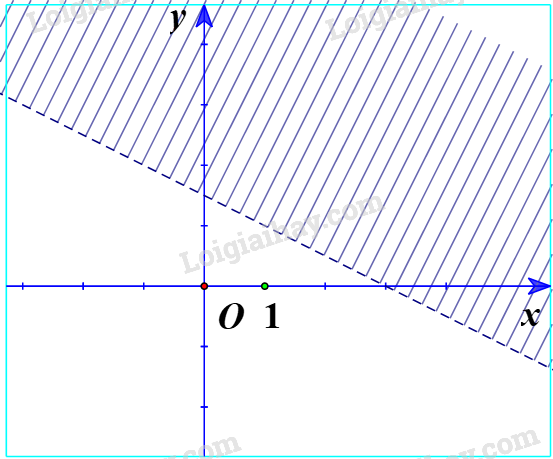
Đề bài

Biểu diễn miền nghiệm của mỗi bất phương trình sau:

a) \(x + 2y < 3\);

b) \(3x - 4y \ge  - 3\);

c) \(y \ge  - 2x + 4\);

d) \(y < 1 - 2x\).

Lời giải chi tiết

a) Ta vẽ đường thẳng d’:\(x + 2y = 3 \Leftrightarrow y =  - \frac{x}{2} + \frac{3}{2}\)

Thay tọa độ điểm O(0;0) vào bất phương trình \(x + 2y < 3\) ta được:

\(0 + 2.0 = 0 < 3\) (Luôn đúng)

Vậy O nằm trong miền nghiệm.

Ta có miền nghiệm:

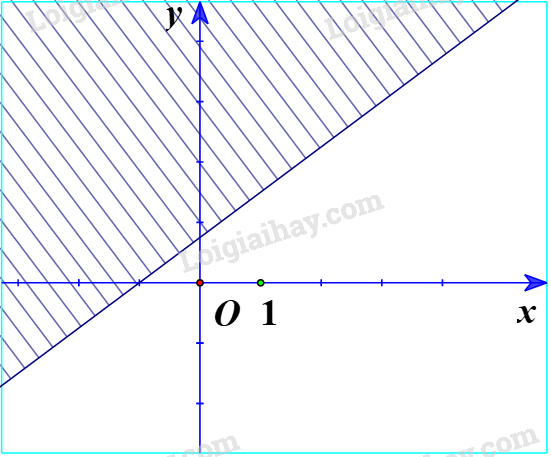
b) Ta vẽ đường thẳng d:\(3x - 4y =  - 3 \Leftrightarrow y = \frac{{3x}}{4} + \frac{3}{4}\)

Thay tọa độ điểm O(0;0) vào bất phương trình \(3x - 4y \ge  - 3\) ta được:

\(3.0 - 4.0 = 0 \ge  - 3\) (Luôn đúng)

Vậy O nằm trong miền nghiệm.

Ta có miền nghiệm:

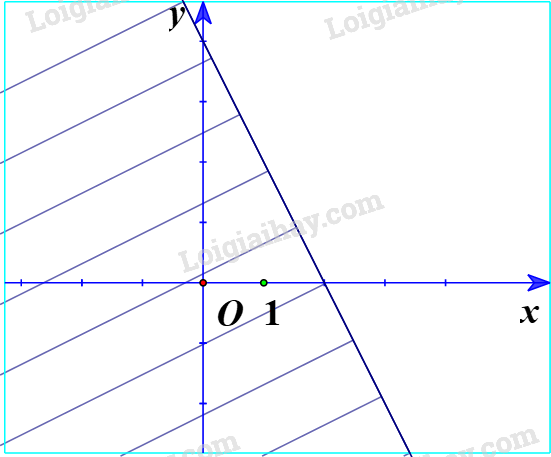
c) Ta vẽ đường thẳng d:\(y =  - 2x + 4\)

Thay tọa độ điểm O(0;0) vào bất phương trình \(y \ge  - 2x + 4\) ta được:

\(0 \ge  - 2.0 + 4 \Leftrightarrow 0 \ge 4\) (Vô lí)

Vậy O không nằm trong miền nghiệm.

Ta có miền nghiệm:

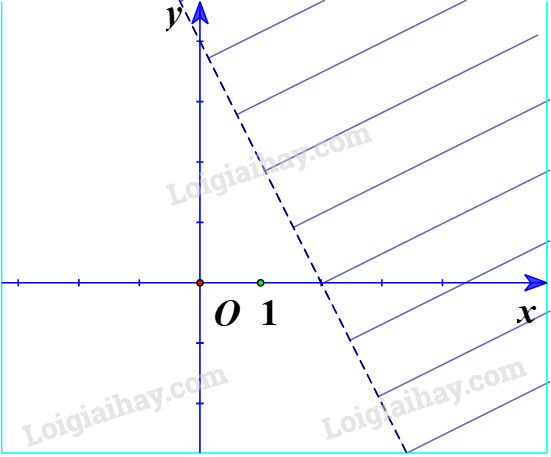
d) Ta vẽ đường thẳng d:\(y = 1 - 2x\)

Thay tọa độ điểm O(0;0) vào bất phương trình \(y < 1 - 2x\) ta được:

\(0 < 1 - 2.0\) (Luôn đúng)

Vậy O nằm trong miền nghiệm.

Ta có miền nghiệm:

Chú ý

Đối với các bất phương trình có dấu “<” hoặc “>” thì vẽ đường thẳng là nét đứt.

Đối với các bất phương trình có dấu “\( \le \)” hoặc “\( \ge \)” thì vẽ đường thẳng là nét liền.