Bài 23 trang 82 SBT toán 8 tập 1Giải bài 23 trang 82 sách bài tập toán 8. Hình thang cân ABCD có AB // CD, O là giao điểm của hai đường chéo. Chứng minh rằng OA=OB, OC=OD. Quảng cáo
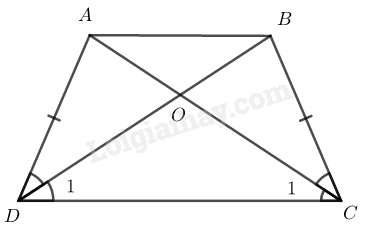
Đề bài Hình thang cân \(ABCD\) có \(AB // CD,\) \(O\) là giao điểm của hai đường chéo. Chứng minh rằng \(OA=OB,\) \(OC=OD.\) Phương pháp giải - Xem chi tiết Ta sử dụng kiến thức: +) Hình thâng cân là hình thang có hai góc kề một đáy bằng nhau. +) Trong hình thang cân, hai cạnh bên bằng nhau. +) Trong hình thang cân, hai đường chéo bằng nhau. Lời giải chi tiết
Xét \(∆ ADC\) và \(∆ BCD,\) ta có: \(AD = BC\) (tính chất hình thang cân) \(\widehat {ADC} = \widehat {BCD}\) (do ABCD là hình thang cân) \(DC\) cạnh chung Do đó: \(∆ ADC = ∆ BCD\;\;\; (c.g.c)\) \( \Rightarrow {\widehat C_1} = {\widehat D_1}\) Trong \(∆ OCD\) ta có: \({\widehat C_1} = {\widehat D_1}\) \(⇒ ∆ OCD\) cân tại \(O\) \(⇒ OC = OD \;\;\;\;(1)\) Do ABCD là hình thang cân nên \(AC = BD\) ( tính chất) \(⇒ AO + OC = BO + OD \;\;\;(2)\) Từ \((1)\) và \((2)\) suy ra: \(AO = BO\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
