Bài 2.3 phần bài tập bổ sung trang 167 SBT toán 8 tập 1Giải bài 2.3 phần bài tập bổ sung trang 167 sách bài tập toán 8. Cho lục giác đều MNPQRS. Gọi X, Y, Z tương ứng là trung điểm của cạnh MN, PQ, RS. Khi đó XYZ là:... Quảng cáo
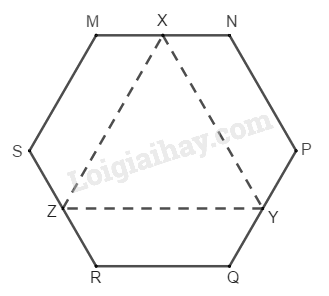
Đề bài Cho lục giác đều \(MNPQRS.\) Gọi \(X,\, Y,\, Z\) tương ứng là trung điểm của cạnh \(MN,\, PQ,\, RS.\) Khi đó \(XYZ\) là: (A) tam giác vuông; (B) tam giác vuông cân; (C) tam giác đều; (D) tam giác mà độ dài các cạnh của nó đôi một khác nhau.
Phương pháp giải - Xem chi tiết Sử dụng tính chất đường trung bình của hình thang bằng nửa tổng hai đáy. Lời giải chi tiết Chọn (C) Do \(MNPQRS\) là lục giác đều nên \(MNPQ\) là hình thang. Ta có \(X,\,Y\) lần lượt là trung điểm của \(MN,\,PQ\) nên \(XY\) là đường trung bình của hình thang \(MNPQ\) Suy ra: \(XY=\dfrac{1}{2} (MQ+NP)\) Tương tự: \(ZY=\dfrac{1}{2} (SP+RQ)\) (\(ZY\) là đường trung bình của hình thang \(RQPS)\) \(XZ=\dfrac{1}{2} (NR+MS)\) (\(XZ\) là đường trung bình của hình thang \(MNRS)\) Mà \(MQ=SP=NR\) và \(NP=RQ=MS\) ( do \(MNPQRS\) là lục giác đều ) Vậy \(XY=ZY=XZ\) hay \(XYZ\) là tam giác đều. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
