Bài 22.1, 22.2, 22.3, 22.4 trang 50 SBT Vật lí 10

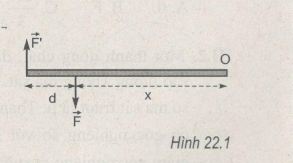
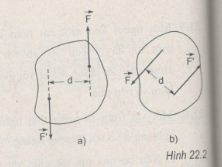
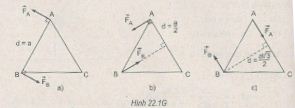
22.1.

Một ngẫu lực (\(\overrightarrow F ,\overrightarrow {F'} \) ) tác dụng vào một thanh cứng như hình 22.1. Momen của ngẫu lực tác dụng vào thanh đối với trục O là bao nhiêu ?

Phương pháp giải:

Áp dụng công thức tính momen của ngẫu lực

\(M = F.d\)

Trong đó:

M: Momen của ngẫu lực

F: độ lớn của mỗi lực

D: cánh tay đòn của ngẫu lực (khoảng cách giữa hai giá của hai lực)

Lời giải chi tiết:

Vì hai lực F'=F; khoảng cách giá của hai lực là d nên áp dụng công thức tính momen ngẫu lực ta có M=F.d

Chọn đáp án D

22.2.

Một cái chắn đường có trọng lượng 600N quay quanh trục nằm ngang O. Trục quay này cũng là trục quay của động cơ điện dùng để nâng chắn đường lên. Trọng tâm G của chắn đường cách O: 50 cm. Để nâng chắn đường lên, momen ngẫu lực của động cơ phải có độ lớn tối thiểu là

A. 300 N.m

B. 150 N.m

C. 1200 N.m

D. 600 N.m

Phương pháp giải:

Áp dụng công thức tính momen của ngẫu lực

\(M = F.d\)

Trong đó:

M: Momen của ngẫu lực

F: độ lớn của mỗi lực

D: cánh tay đòn của ngẫu lực (khoảng cách giữa hai giá của hai lực)

Lời giải chi tiết:

\({M_F} = {M_P} = Pd = 600.0,5 = 300N.m\)

Chọn đáp án A

22.3.

Tác dụng của ngẫu lực đối với một vật có thay đổi không nếu ta thay đổi điểm đặt và phương của cặp lực (F, F') nhưng không thay đổi độ lớn của lực và cánh tay đòn của ngẫu lực (H.22.2 a và b) ?

Phương pháp giải:

Sử dụng lí thuyết về momen ngẫu lực: momen của ngẫu lực không phụ thuộc vào vị trí của trục quay vuông góc với mặt phẳng chứa ngẫu lực

Lời giải chi tiết:

Vì momen của ngẫu lực không phụ thuộc vào vị trí của trục quay vuông góc với mặt phẳng chứa ngẫu lực và 

công thức tính momen của ngẫu lực

\(M = F.d\)

Trong đó:

M: Momen của ngẫu lực

F: độ lớn của mỗi lực

d: cánh tay đòn của ngẫu lực (khoảng cách giữa hai giá của hai lực)

Vậy nên tác dụng của ngẫu lực đối với một vật không thay đổi nếu ta thay đổi điểm đặt và phương của cặp lực (F, F') nhưng không thay đổi độ lớn của lực và cánh tay đòn của ngẫu lực

22.4.

Một vật rắn phẳng, mỏng có dạng là một tam giác đều ABC, mỗi cạnh là a = 20 cm. Người ta tác dụng vào vật một ngẫu lực nằm trong mặt phẳng của tam giác. Các lực có độ lớn là 8 N và đặt vào hai đỉnh A và B. Tính momen của ngẫu lực trong các trường hợp sau đây :

a) Các lực vuông góc với cạnh AB.

b) Các lực vuông góc với cạnh AC.

c) Các lực song song với cạnh AC.

Phương pháp giải:

Áp dụng công thức tính momen của ngẫu lực

\(M = F.d\)

Trong đó:

M: Momen của ngẫu lực

F: độ lớn của mỗi lực

d: cánh tay đòn của ngẫu lực (khoảng cách giữa hai giá của hai lực)

Lời giải chi tiết:

Áp dụng công thức tính momen ngẫu lực M = F.d vào các phần ta được

a. M = F.d = F.a = 8.0,2 = 1,6 N.m

b. M = F.d = F.a/2 = 8.0,1 = 0,8 N.m

c. M = F.d = F.\(\displaystyle a{{\sqrt 3 } \over 2}\)

= 8. 0,1\(\displaystyle{{\sqrt 3 } \over 2}\) = 1,38 N.m

Loigiaihay.com