Giải bài 2 (10.21) trang 102 vở thực hành Toán 7 tập 2Tính thể tích, diện tích xung quanh, diện tích toàn phần của hình hộp chữ nhật và hình lăng trụ trong Hình 10.21. Quảng cáo
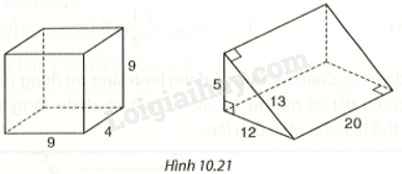
Đề bài Tính thể tích, diện tích xung quanh, diện tích toàn phần của hình hộp chữ nhật và hình lăng trụ trong Hình 10.21.
Phương pháp giải - Xem chi tiết + Thể tích hình hộp chữ nhật: \(V = a.b.c\) với a, b, c lần lượt là chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật đó. + Thể tích của hình lăng trụ đứng tam giác: \(V = \) Sđáy.h, trong đó V là thể tích của hình lăng trụ đứng, Sđáy là diện tích một đáy của hình lăng trụ đứng, h là chiều cao của hình lăng trụ đứng. + Diện tích xung quanh của hình lăng trụ đứng tam giác, hình lăng trụ đứng tứ giác: \({S_{xq}} = \) Cđáy.h, trong đó \({S_{xq}}\) là diện tích xung quanh của hình lăng trụ đứng, Cđáy là chu vi một đáy của hình lăng trụ đứng, h là chiều cao của hình lăng trụ đứng. + Diện tích xung quanh hình hộp chữ nhật: \({S_{xq}} = 2\left( {a + b} \right).c\) với a, b, c lần lượt là chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật đó. + Diện tích toàn phần= diện tích xung quanh+ diện tích hai đáy. Lời giải chi tiết
Diện tích xung quanh của hình hộp chữ nhật là: \({S_{xq}} = 2.\left( {9 + 4} \right).9 = 234\) Diện tích toàn phần của hình hộp chữ nhật là: \({S_{tp}} = 234 + 2.9.4 = 306\)
Diện tích xung quanh của hình lăng trụ đứng tam giác là: \({S_{xq}} = \left( {5 + 12 + 13} \right).20 = 600\) Diện tích toàn phần của hình lăng trụ đứng tam giác là: \({S_{tp}} = 600 + 2.\left( {\frac{1}{2}.5.12} \right) = 660\)  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K12 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
