Bài 145 trang 98 SBT Toán 8 tập 1

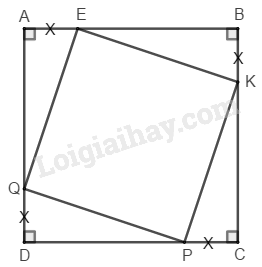
Đề bài

Cho hình vuông \(ABCD.\) Trên các cạnh \(AB,\, BC,\, CD,\, DA\) lấy theo thứ tự các điểm \(E,\, K,\, P,\, Q\) sao cho \(AE = BK = CP = DQ.\) Tứ giác \(EKPQ\) là hình gì ? Vì sao ?

Lời giải chi tiết

Ta có \(AB = BC = CD = DA\) (do ABCD là hình chữ nhật)

Mà \(AE = BK = CP = DQ\) (gt)

Nên \(AB - AE = BC - BK\)\( = CD - CP = DA - DQ\)

Suy ra: \(EB = KC = PD = QA\)

- Xét \(∆ AEQ\) và \(∆ BKE :\)

\(AE = BK\) (gt)

\(\widehat A = \widehat B = {90^0}\)

\(QA = EB\) (chứng minh trên)

Do đó: \(∆ AEQ = ∆ BKE\, (c.g.c)\) \(⇒ EK = EQ\) (1)

- Xét \(∆ BKE\) và \(∆ CPK :\)

\(BK = CP\) (gt)

\(\widehat B = \widehat C = {90^0}\)

\(EB = KC\) (chứng minh trên)

Do đó: \(∆ BKE = ∆ CPK\, (c.g.c)\) \(⇒ EK = KP\) (2)

Xét \(∆ CPK\) và \(∆ DQP :\)

\(CP = DQ\) (gt)

\(\widehat C = \widehat D = {90^0}\)

\(DP = CK\) (chứng minh trên)

Do đó: \(∆ CPK = ∆ DQP\, (c.g.c)\) \(⇒ KP = PQ\) (3)

Từ (1), (2) và (3) suy ra: \(EK = KP = PQ = EQ\)

Tứ giác \(EKPQ\) là hình thoi.

Mặt khác, do  \(∆ AEQ = ∆ BKE\, \) (chứng minh trên) nên \(\widehat {BEK} = \widehat {EQA}\)

Xét tam giác EAQ vuông tại A, ta có \(\widehat {QEA} + \widehat {EQA} = {90^0}\)

Nên \(\widehat {QEA} + \widehat {KEB} = {90^0}\)

Lại có:

\(\begin{array}{l}
\widehat {QEA} + \widehat {QEK} + \widehat {KEB} = {180^0}\\
\Rightarrow \widehat {QEK} = {180^0} - \left( {\widehat {QEA} + \widehat {KEB}} \right)\\
\Rightarrow \widehat {QEK} = {180^0} - {90^0} = {90^0}
\end{array}\)

Từ đó hình thoi \(EKPQ\) có 1 góc vuông nên \(EKPQ\) là hình vuông.

Loigiaihay.com