Bài 11.2 phần bài tập bổ sung trang 97 SBT Toán 8 tập 1

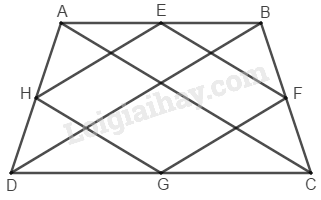
Đề bài

Cho hình thang cân \(ABCD\) \((AB // CD).\) Gọi \(E,\, F,\, G,\, H\) theo thứ tự là trung điểm của các cạnh \(AB,\, BC,\, CD,\, DA.\) Tứ giác \(EFGH\) là hình gì ?

Lời giải chi tiết

Trong \(∆ ABD\) ta có:

\(E\) là trung điểm của \(AB\) (gt)

\(H\) là trung điểm của \(AD\) (gt)

nên \(EH\) là đường trung bình của \(∆ ABD\)  

\(⇒ EH // BD\) và \(EH = \displaystyle {1 \over 2}BD\) (tính chất đường trung bình của tam giác) (1)

- Trong \(∆ CBD\) ta có:

\(F\) là trung điểm của \(BC\) (gt)

\(G\) là trung điểm của \(CD\) (gt)

nên \(FG\) là đường trung bình của \(∆ CBD\)

\(⇒ FG // BD\) và \(FG = \displaystyle {1 \over 2}BD\) (tính chất đường trung bình của tam giác) (2)  

Từ (1) và (2) suy ra: \(EH // FG\) và \(EH = FG\)

Suy ra: Tứ giác \(EFGH\) là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)

Trong \(∆ ABC\) ta có:

\(E\) là trung điểm của \(AB\) (gt)

\(F\) là trung điểm của \(BC\) (gt)

Nên \(EF\) là đường trung bình của \(∆ ABC\)

\(⇒ EF = \displaystyle {1 \over 2}AC\) (tính chất đường trung bình của tam giác) (3)

\(AC = BD\) (tính chất hình thang cân) (4)

Từ (1), (3) và (4) suy ra: \(EH = EF\)

Vậy : Tứ giác \(EFGH\) là hình thoi.

Loigiaihay.com