Lý thuyết Giải tam giác. Tính diện tích tam giác - SGK Toán 10 Cánh diềuA. Lý thuyết 1. Giải tam giác Quảng cáo
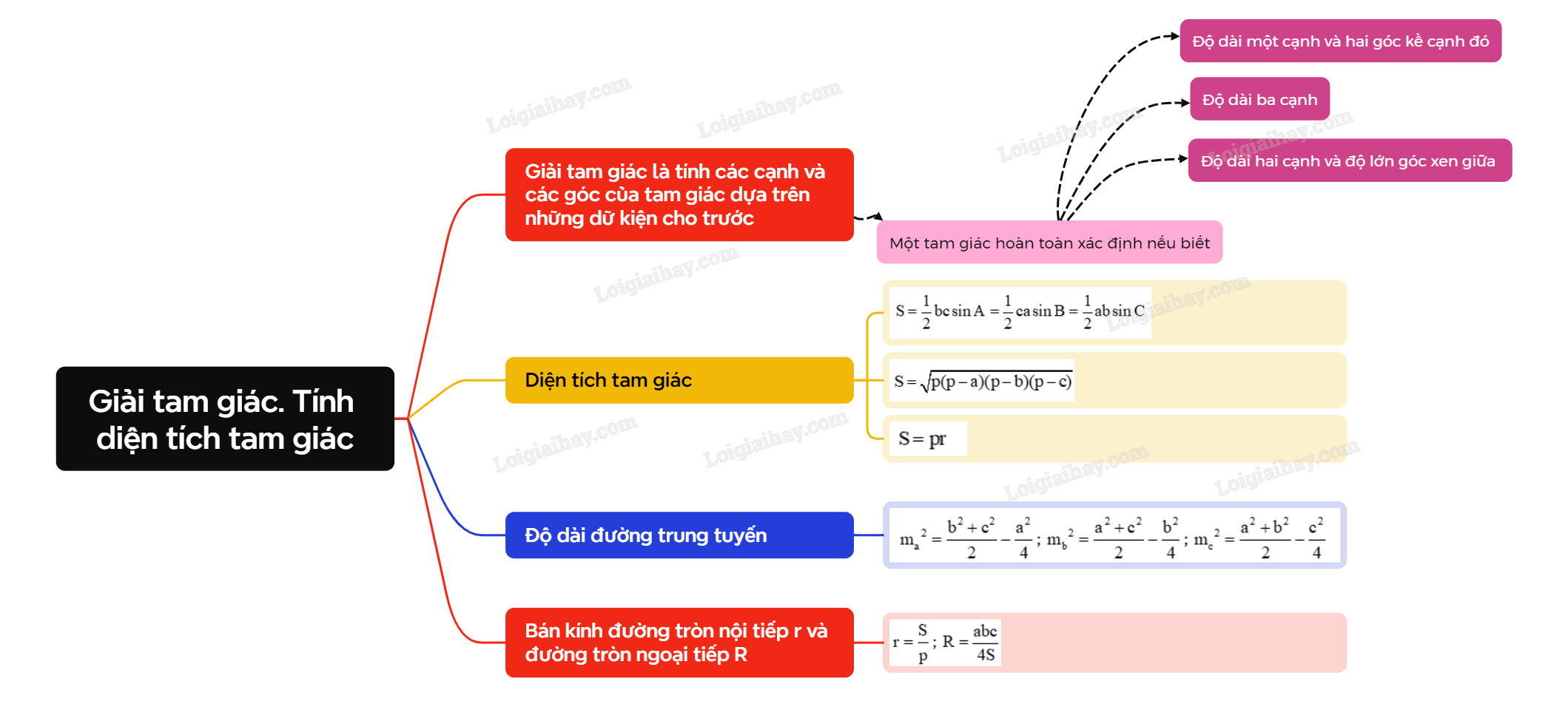
A. Lý thuyết 1. Giải tam giác
Một tam giác hoàn toàn xác định nếu biết một trong các dữ kiện: - Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó. - Biết độ dài ba cạnh. - Biết độ dài một cạnh và hai góc kề cạnh đó. 2. Tính diện tích tam giác
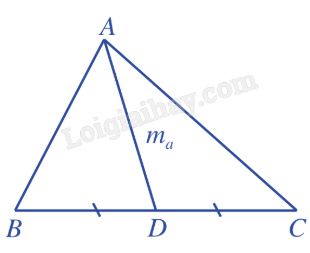
3. Áp dụng vào bài toán thực tiễn Sử dụng các hệ thức lượng đã học, định lí sin, côsin, công thức tính diện tích tam giác để áp dụng vào các bài toán thực tiễn. * Tìm hiểu thêm Cho tam giác ABC có AB = c, AC = b, BC = a. Gọi R, r, p và S lần lượt là bán kính đường tròn ngoài tiếp, bán kính đường tròn nội tiếp, nửa chu vi và diện tích của tam giác ABC. a) Công thức độ dài đường trung tuyến
b) Công thức tính bán kính đường tròn nội tiếp và bán kính đường tròn ngoại tiếp tam giác
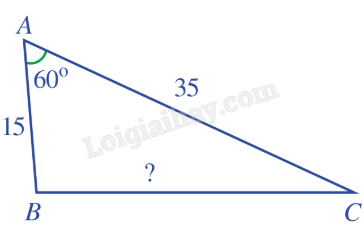
B. Bài tập Bài 1: Cho tam giác ABC có: a) AB = 15, AC = 35, \(\widehat A = {60^o}\). Tính cạnh BC.
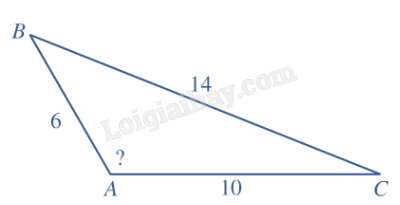
Giải: Áp dụng định lí côsin trong tam giác ABC, ta có: \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC\cos A = {15^2} + {35^2} - 2.15.35.\cos {60^o} = 925\). Do đó \(BC = \sqrt {925} \approx 30,4\). b) AB = 6, AC = 10, BC = 14. Tính góc A.
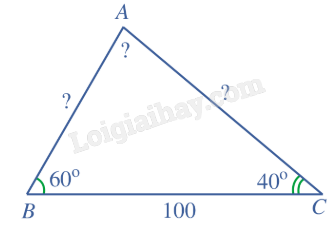
Giải: Áp dụng định lí côsin trong tam giác ABC, ta có: \(\cos A = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}} = \frac{{{6^2} + {{10}^2} - {{14}^2}}}{{2.6.10}} = - 0,5\). Do đó \(\widehat A = {120^o}\). c) BC = 100, \(\widehat B = {60^o}\), \(\widehat C = {40^o}\). Tính góc A và các cạnh AB, AC (làm tròn kết quả đến hàng phần mười).
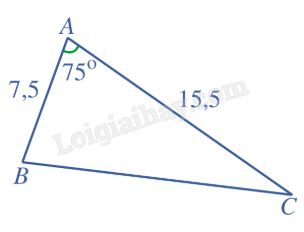
Giải: Ta có \(\widehat A = {180^o} - \left( {\widehat B + \widehat C} \right) = {180^o} - \left( {{{60}^o} + {{40}^o}} \right) = {80^o}\). Áp dụng định lí sin trong tam giác ABC, ta có: \(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} = \frac{{CA}}{{\sin B}}\). Do đó: \(AB = \frac{{BC\sin C}}{{\sin A}} = \frac{{100\sin {{40}^o}}}{{\sin {{80}^o}}} \approx 65,3\). \(AC = \frac{{BC\sin B}}{{\sin A}} = \frac{{100\sin {{60}^o}}}{{\sin {{80}^o}}} \approx 87,9\). Bài 2: Cho tam giác ABC có AB = 7,5, AC = 15,5, \(\widehat A = {75^o}\). Tính diện tích S của tam giác ABC (làm tròn kết quả đến hàng phần mười).
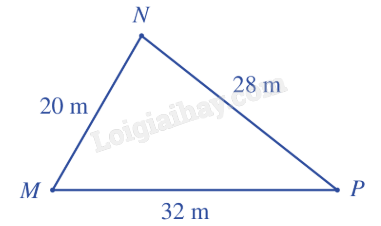
Giải: Ta có \(S = \frac{1}{2}AB.AC\sin A = \frac{1}{2}.7,5.15,5.\sin {75^o} \approx 56,1\). Bài 3: Mảnh vườn hình tam giác gia đình bạn Nam có chiều dài các cạnh là MN = 20 m, NP = 28 m, MP = 32 m. Hỏi diện tích mảnh vườn của gia đình bạn Nam là bao nhiêu mét vuông (làm tròn đến hàng phần mười)?
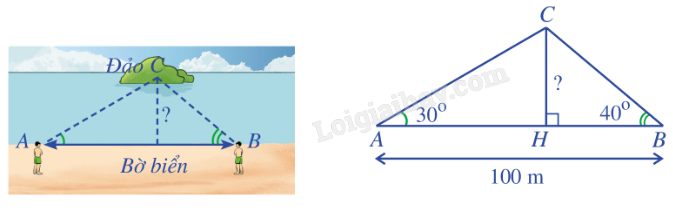
Giải: Ta có \(p = \frac{{20 + 28 + 32}}{2} = 40\) (m). Diện tích mảnh vườn là: \(S = \sqrt {40(40 - 20)(40 - 28)(40 - 32)} \approx 277,1\) \(({m^2})\). Bài 4: Đứng ở vị trí A trên bờ biển, bạn Minh đo được góc nghiêng so với bờ biển tới một vị trí C trên đảo là 30°. Sau đó đi chuyển dọc bờ biển đến vị trí B cách A một khoảng 100 m và đo được góc nghiêng so với bờ biển tới vị trí C đã chọn là 40°. Tính khoảng cách từ vị trí C trên đảo tới bờ biển theo đơn vị mét (làm tròn kết quả đến hàng phần mười).
Giải: Xét tam giác ABC, có \(\widehat C = {180^o} - \left( {\widehat B + \widehat A} \right) = {180^o} - \left( {{{40}^o} + {{30}^o}} \right) = {110^o}\). Áp dụng định lí sin trong tam giác ABC: \(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\). Do đó \(AC = \frac{{AB\sin B}}{{\sin C}} = \frac{{100\sin {{40}^o}}}{{\sin {{110}^o}}} \approx 68,4\) (m). Xét tam giác vuông AHC có \(CH = AC\sin {30^o} \approx 68,4.0,5 \approx 34,2\) (m). Vậy khoảng cách từ vị trí C trên đảo tới bờ biển xấp xỉ 34,2 m.
|




















Danh sách bình luận