Giải mục III trang 89, 90 SGK Toán 10 tập 1 - Cánh diều

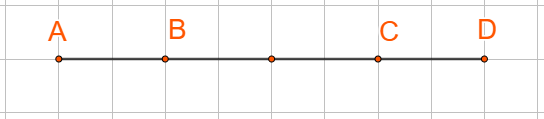
Hoạt động 3

Cho I là trung điểm của đoạn thẳng AB và điểm M tuỳ ý. Chứng minh rằng $\overrightarrow{MA} + \overrightarrow{MB} = 2\overrightarrow{MI}$. 

Phương pháp giải:

Áp dụng quy tắc ba điểm.

Lời giải chi tiết:

$\overrightarrow{MA} + \overrightarrow{MB} = (\overrightarrow{MI} + \overrightarrow{IA}) + (\overrightarrow{MI} + \overrightarrow{IB}) = 2\overrightarrow{MI} + (\overrightarrow{IA} + \overrightarrow{IB}) = 2\overrightarrow{MI} + \overrightarrow{0} = 2\overrightarrow{MI}$.

Hoạt động 4

Cho G là trọng tâm của tam giác ABC và điểm M tuỳ ý. Chứng minh rằng $\overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} = 3\overrightarrow{MG}$. 

Phương pháp giải:

Áp dụng quy tắc ba điểm.

Lời giải chi tiết:

Để chứng minh đẳng thức trên, ta làm như sau: $\overrightarrow{MA} + \overrightarrow{MB} + \overrightarrow{MC} = (\overrightarrow{MG} + \overrightarrow{GA}) + (\overrightarrow{MG} + \overrightarrow{GB}) + (\overrightarrow{MG} + \overrightarrow{GC})$ $= 3\overrightarrow{MG} + (\overrightarrow{GA} + \overrightarrow{GB} + \overrightarrow{GC}) = 3\overrightarrow{MG} + \overrightarrow{0} = 3\overrightarrow{MG}$.

LT-VD 3

Cho tam giác ABC có G là trọng tâm. Chứng minh \(\overrightarrow {AB}  + \overrightarrow {AC}  = 3\overrightarrow {AG} \).

Phương pháp giải:

G là trọng tâm tam giác ABC thì \(\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  = 3\overrightarrow {MG} \) với điểm M bất kì.

Lời giải chi tiết:

Với điểm M bất kì ta có: \(\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  = 3\overrightarrow {MG} \).

Chọn M trùng A, ta được:

\(\overrightarrow {AA}  + \overrightarrow {AB}  + \overrightarrow {AC}  = 3\overrightarrow {AG}  \Leftrightarrow \overrightarrow {AB}  + \overrightarrow {AC}  = 3\overrightarrow {AG} \).

Hoạt động 5

Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ khác $\overrightarrow{0}$ sao cho $\overrightarrow{a} = k\overrightarrow{b}$ với $k$ là số thực khác $0$. Nêu nhận xét về phương của hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$.

Lời giải chi tiết:

Hai vecto $\overrightarrow{a}$ và $\overrightarrow{b}$ cùng phương.

Hoạt động 6

Cho ba điểm phân biệt A, B, C.

a) Nếu ba điểm A, B, C thẳng hàng thì hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương hay không?

b) Ngược lại, nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì ba điểm A, B, C có thẳng hàng hay không?

Phương pháp giải:

Hai vecto được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Lời giải chi tiết:

a) Nếu A, B, C thẳng hàng thì đường thẳng AB trùng đường thẳng AC, do đó hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương.

b) Nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì đường thẳng AB trùng đường thẳng AC, do đó ba điểm A, B, C có thẳng hàng.

LT-VD 4

Ở hình 61, tìm k trong mỗi trường hợp sau:

a) \(\overrightarrow {AC}  = k.\overrightarrow {AD} \);

b) \(\overrightarrow {BD}  = k.\overrightarrow {DC} \).

Phương pháp giải:

Từ hình vẽ suy ra hướng và tỉ số độ dài của hai vecto.

Lời giải chi tiết:

a) Ta có: \(\overrightarrow {AC} ,\overrightarrow {AD} \) là hai vecto cùng hướng và \(\left| {\overrightarrow {AC} } \right| = \frac{3}{4}\left| {\overrightarrow {AD} } \right|\).

Suy ra \(\overrightarrow {AC}  = \frac{3}{4}\overrightarrow {AD} .\) Vậy \(k = \frac{3}{4}\).

b) Ta có: \(\overrightarrow {BD} ,\overrightarrow {DC} \) là hai vecto ngược hướng và \(\left| {\overrightarrow {BD} } \right| = 3\left| {\overrightarrow {DC} } \right|\).

Suy ra \(\overrightarrow {BD}  =  - 3\overrightarrow {DC} \). Vậy \(k =  - 3\).