Giải mục II trang 39, 40, 41, 42 SGK Toán 10 tập 1 - Cánh diềua) Tìm giá trị y tương ứng với giá trị của x trong bảng sau: Tổng hợp đề thi giữa kì 2 lớp 10 tất cả các môn - Cánh diều Toán - Văn - Anh - Lí - Hóa - Sinh Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
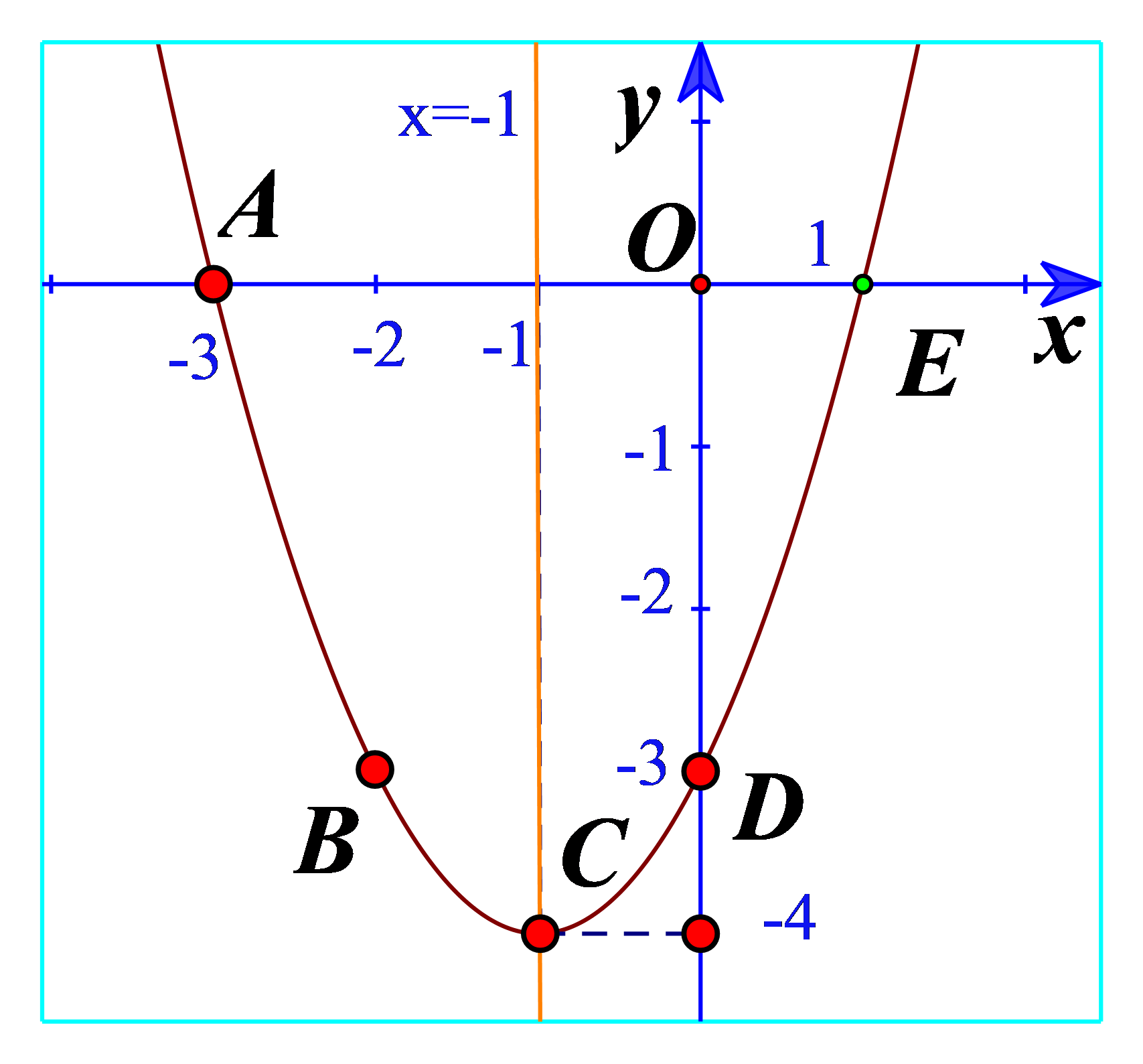
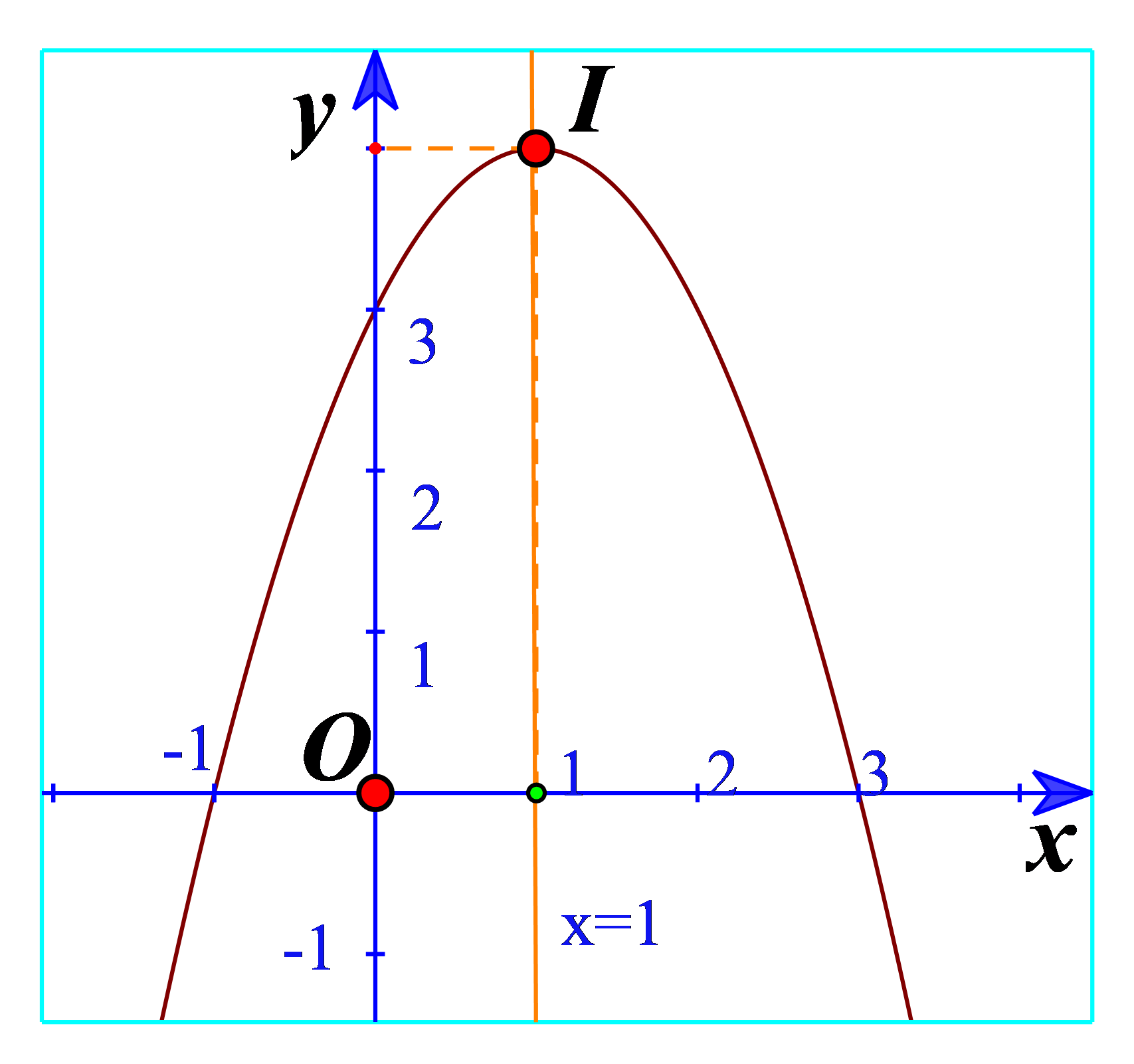
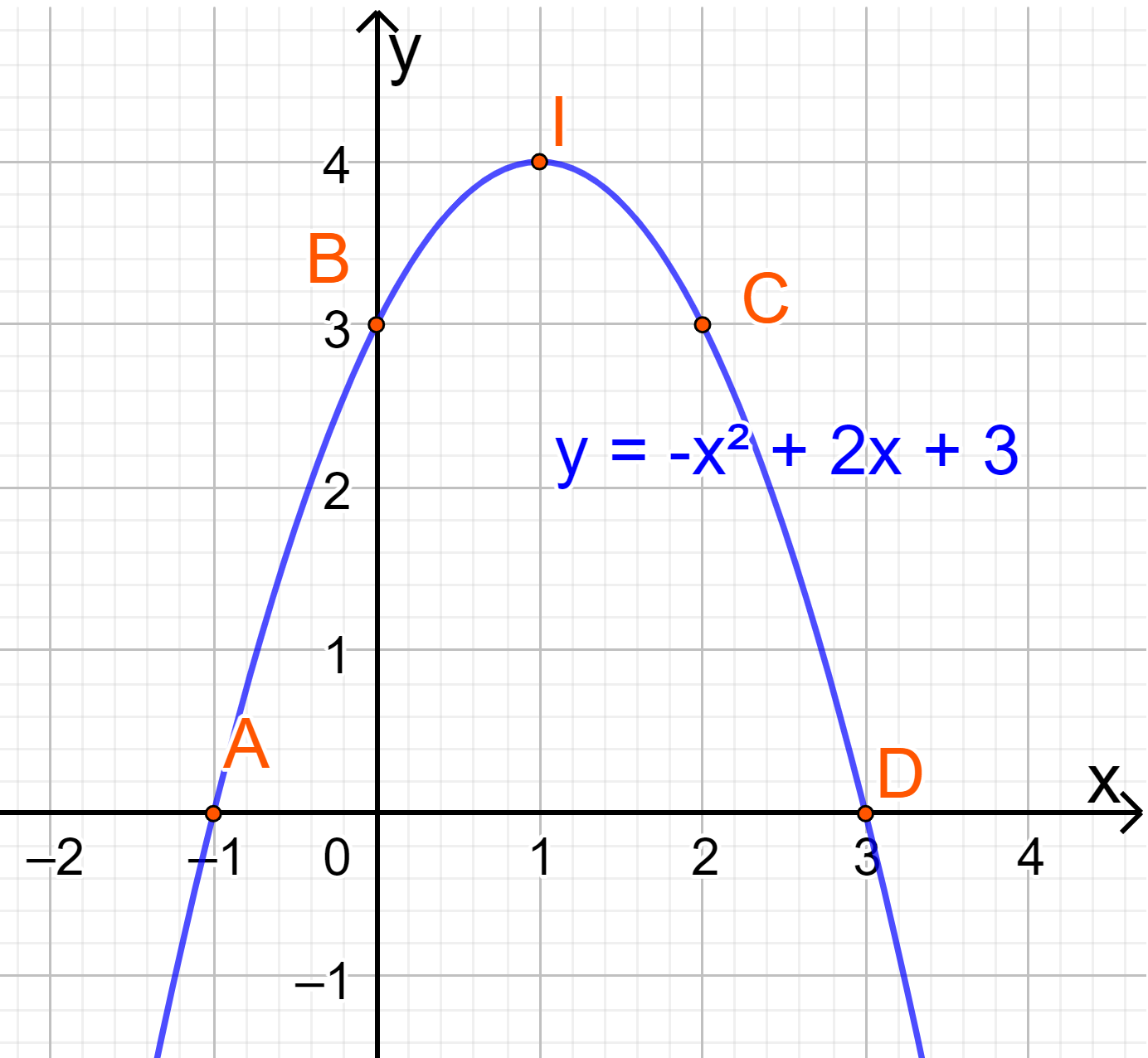
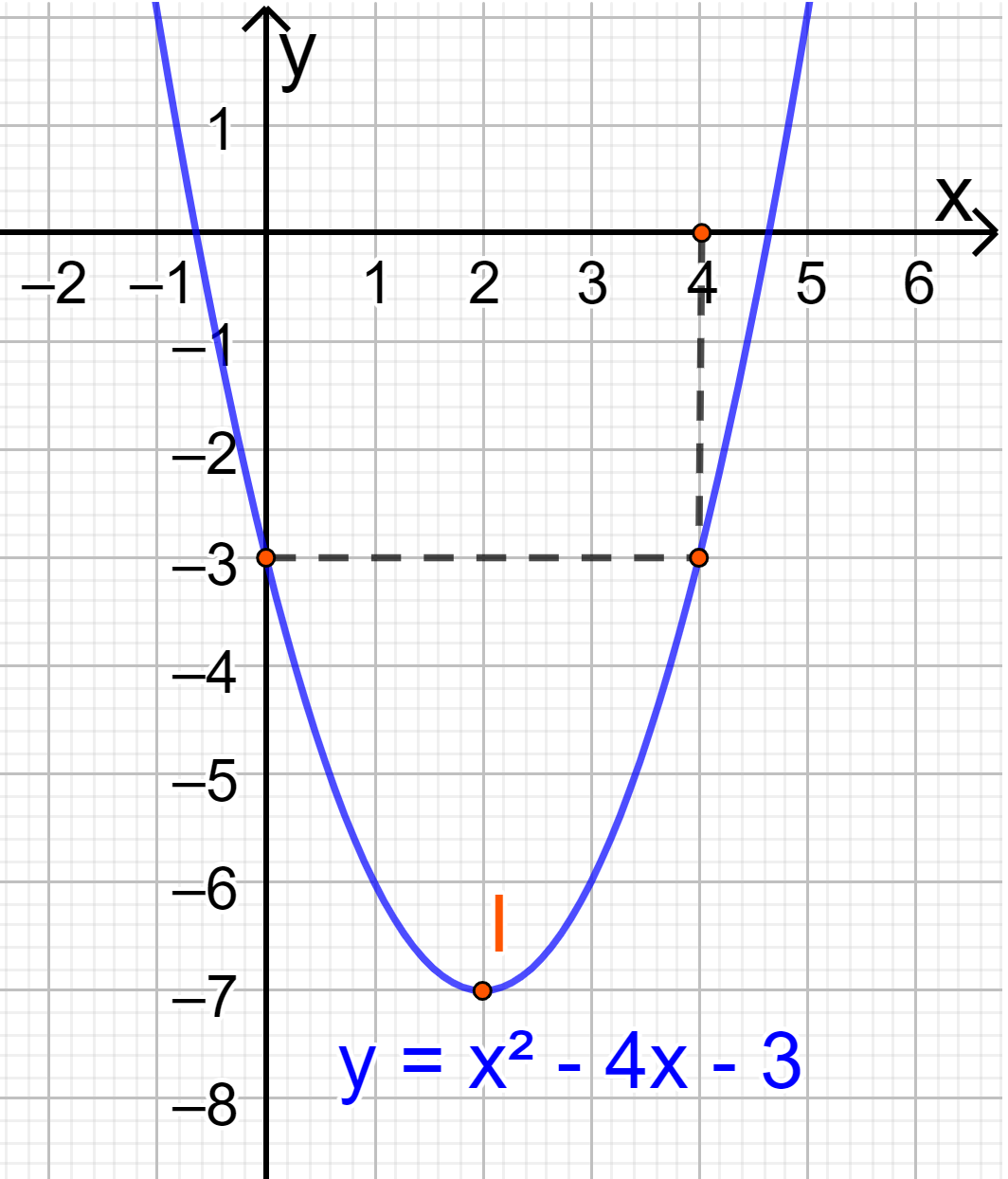
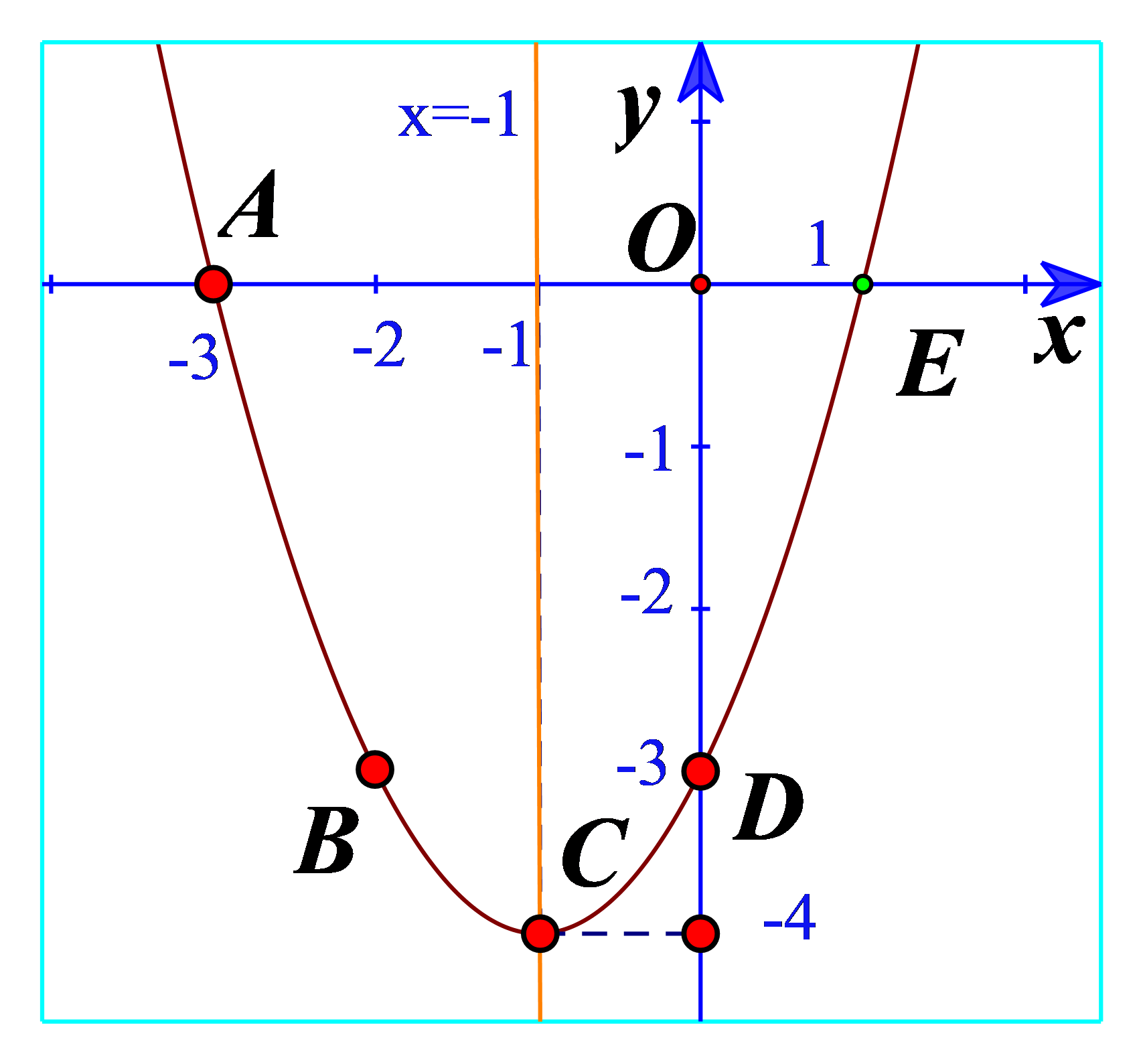
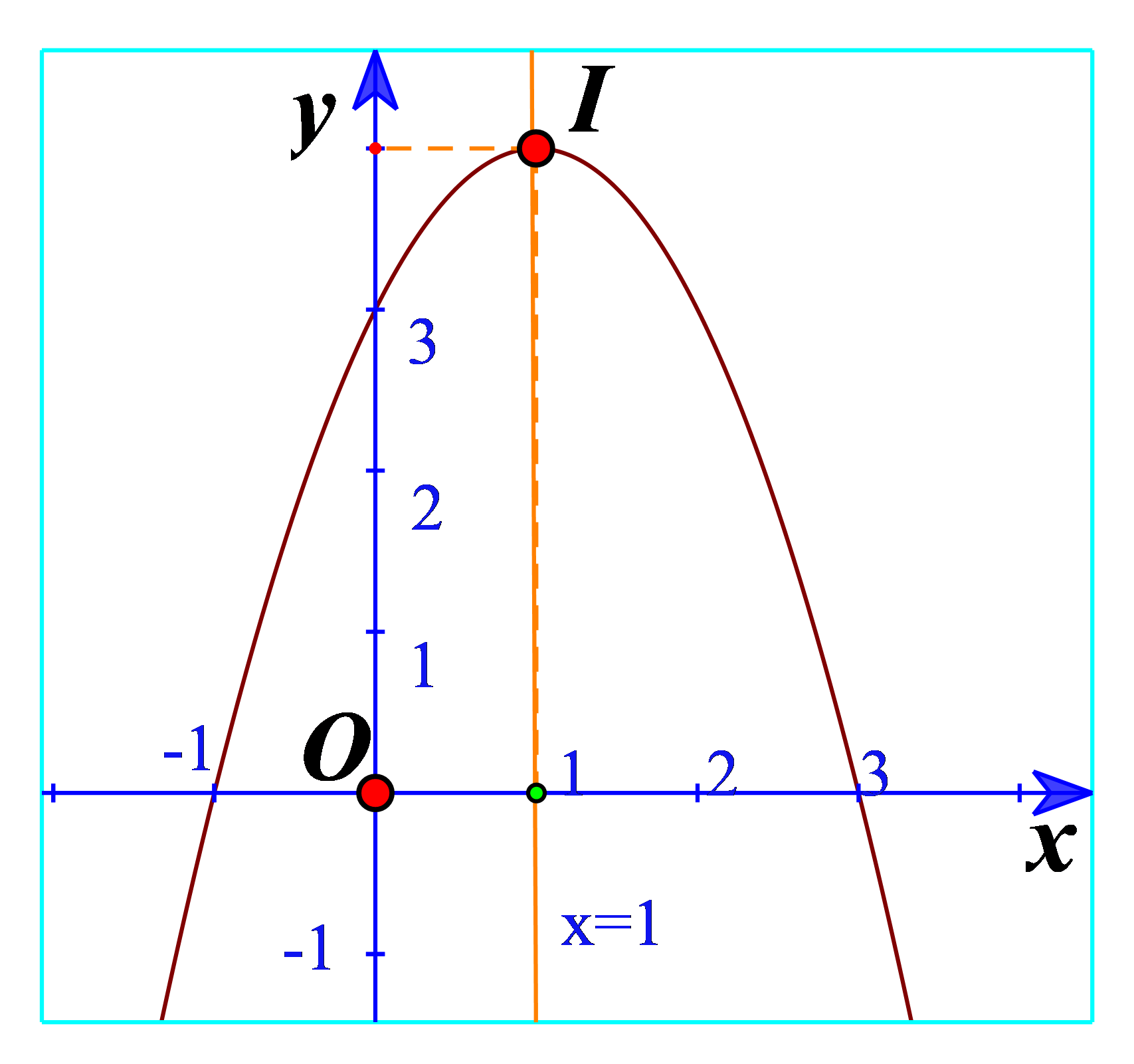
Hoạt động 2 Cho hàm số \(y = {x^2} + 2x - 3\). a) Tìm giá trị y tương ứng với giá trị của x trong bảng sau: b) Vẽ các điểm \(A\left( { - 3;0} \right),B\left( { - 2; - 3} \right),C\left( { - 1; - 4} \right),\)\(D\left( {0; - 3} \right),E\left( {1;0} \right)\) của đồ thị hàm số \(y = {x^2} + 2x - 3\) trong mặt phẳng tọa độ Oxy. c) Vẽ đường cong đi qua 5 điểm A, B, C, D, E. Đường cong đó là đường parabol và cũng chính là đồ thị hàm số \(y = {x^2} + 2x - 3\) (Hình 11). d) Cho biết tọa độ của điểm thấp nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới? Phương pháp giải: a) Thay \(x = - 3,x = - 2,x = - 1,\)\(x = 0,x = 1\) vào hàm số. b) Xác định các điểm trên mặt phẳng. c) Sử dụng thước hoặc công cụ khác để vẽ đồ thị nối 5 điểm. d) Tìm điểm thấp nhất trên hình vẽ và đường thẳng x=a với a là hoành độ của điểm thấp nhất. Lời giải chi tiết: a) Thay \(x = - 3\) vào hàm số ta được: \(y = {\left( { - 3} \right)^2} + 2.\left( { - 3} \right) - 3 = 0\). Điền 0 vào ô tương ứng. Thay \(x = - 2\) vào hàm số ta được: \(y = {\left( { - 2} \right)^2} + 2.\left( { - 2} \right) - 3 = - 3\). Điền \( - 3\) vào ô tương ứng. Thay \(x = - 1\) vào hàm số ta được: \(y = {\left( { - 1} \right)^2} + 2.\left( { - 1} \right) - 3 = - 4\). Điền \( - 4\) vào ô tương ứng. Thay \(x = 0\) vào hàm số ta được: \(y = - 3\). Điền \( - 3\) vào ô tương ứng. Thay \(x = 1\) vào hàm số ta được: \(y = {\left( 1 \right)^2} + 2.\left( 1 \right) - 3 = 0\). Điền 0 vào ô tương ứng. Vậy ta có: b) Các điểm có trong hình 11. c) Đường cong đi qua 5 điểm là parabol trong hình 11. d) Từ đồ thị ta thấy điểm thấp nhất là điểm C(-4;-1) Phương trình trục đối xứng là x=-1 Đồ thị có bề lõm lên trên. Hoạt động 3 Cho hàm số \(y = - {x^2} + 2x + 3\). a) Tìm tọa độ 5 điểm thuộc đồ thị hàm số trên có hoành độ lần lượt là \( - 1,0,1,2,3\) rồi vẽ chúng trong mặt phẳng tọa độ Oxy. b) Vẽ đường cong đi qua 5 điểm trên. Đường cong đó cũng là đường parabol và là đồ thị của hàm số \(y = - {x^2} + 2x + 3\) (Hình 12). c) Cho biết tọa độ của điểm cao nhất và phương trình trục đối xứng của parabol đó. Đồ thị hàm số đó quay bề lõm lên trên hay xuống dưới? Phương pháp giải: a) Lần lượt thay \( - 1,0,1,2,3\) vào biểu thức của hàm số để tìm tung độ => Biểu diễn các điểm trên mặt phẳng tọa độ b) Vẽ đường cong đi qua 5 điểm trên. c) Tìm tọa độ của điểm cao nhất và phương trình trục đối xứng của parabol. Xác định bề lõm. Lời giải chi tiết: a) x=-1 => y=0 x=0 => y=3 x=1=> y= 4 x=2 => y=3 x=3 => y=0 lần lượt là: A(-1;0), B(0;3), I(1;4), C(2;3), D(3;0) b) Vẽ đồ thị: c) Điểm cao nhất là điểm I(1;4) Phương trình trục đối xứng là đường thẳng x=1. Đồ thị hàm số đó quay bề lõm xuống dưới. Luyện tập – vận dụng 2 Vẽ đồ thị mỗi hàm số bậc hai sau: a) \(y = {x^2} - 4x - 3\) b) \(y = {x^2} + 2x + 1\) c) \(y = - {x^2} - 2\) Phương pháp giải: Bước 1: Xác định tọa độ đỉnh \(\left( {\frac{{ - b}}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\) Bước 2: Vẽ trục đối xứng \(x = - \frac{b}{{2a}}\) Bước 3: Xác định một số điểm đặc biệt, chẳng hạn giao điểm với trục tung (0;c) và trục hoành (nếu có), điểm đối xứng với điểm (0;c) qua trục \(x = - \frac{b}{{2a}}\). Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số \(y = a{x^2} + bx + c\). Lời giải chi tiết: a) Đồ thị hàm số có đỉnh \(I\left( {2; - 7} \right)\) Trục đối xứng là x=2 Giao điểm của parabol với trục tung là (0;-3) Điểm đối xứng với điểm (0;-3) qua trục đối xứng x=2 là (4;-3) Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
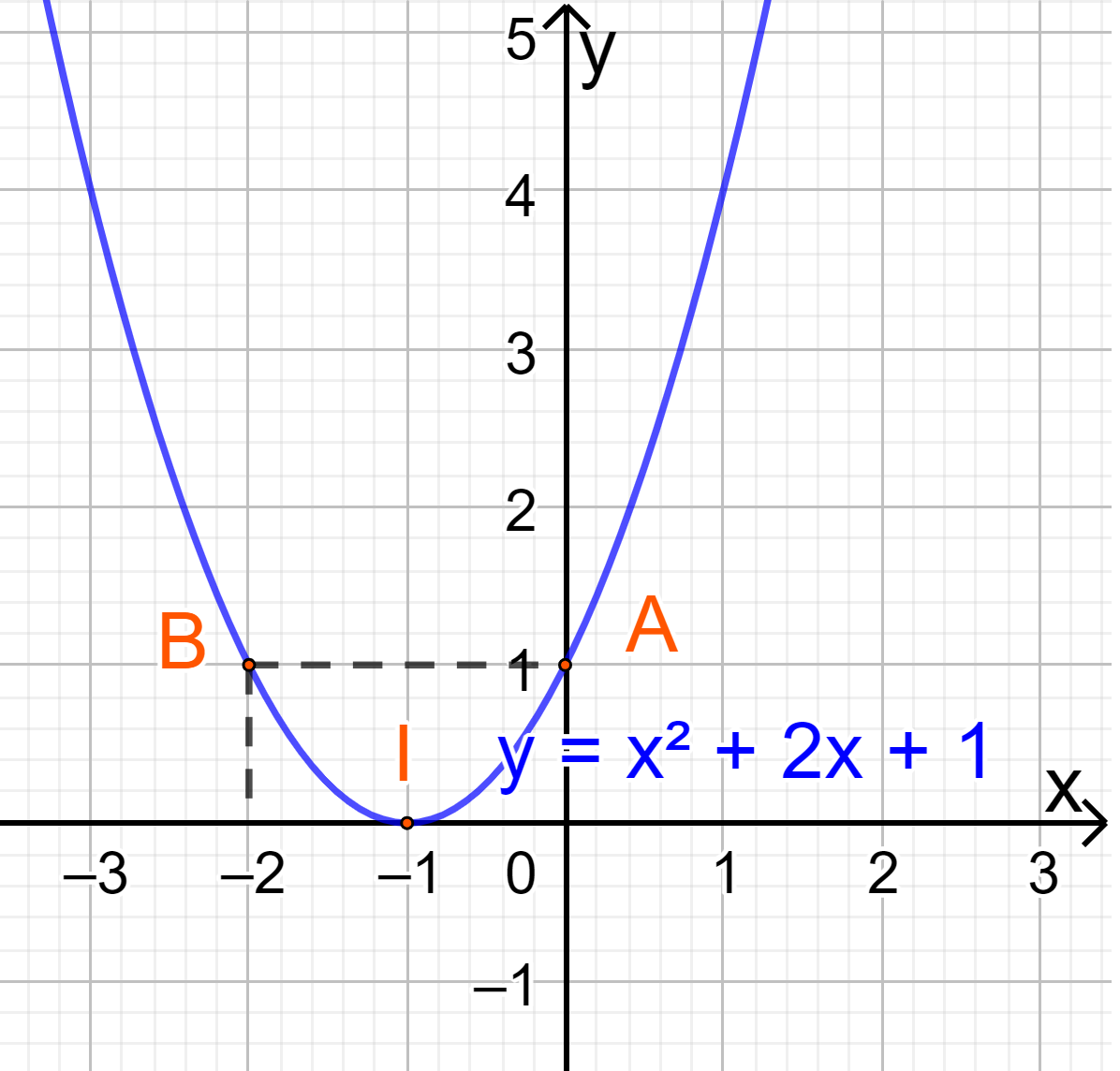
b) Đồ thị hàm số có đỉnh \(I\left( { - 1;0} \right)\) Trục đối xứng là x=-1 Giao điểm của parabol với trục tung là (0;1) Giao điểm của parabol với trục hoành là (-1;0) Điểm đối xứng với điểm (0;1) qua trục đối xứng x=-1 là (-2;1) Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
c) Đồ thị hàm số có đỉnh \(I\left( {0; - 2} \right)\) Trục đối xứng là x=0 Giao điểm của parabol với trục tung là (0;-2) Cho x=1=>y=-3 => Điểm A(1;-3) thuộc đồ thị. Điểm đối xứng với A qua trục đối xứng x=0 là điểm B(-1;-3). Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
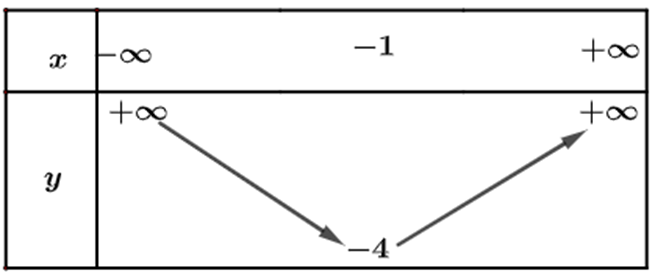
Hoạt động 4 a) Quan sát đồ thị hàm số bậc hai \(y = {x^2} + 2x - 3\) trong Hình 11. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó. b) Quan sát đồ thị hàm số bậc hai \(y = - {x^2} + 2x + 3\) trong Hình 12. Xác định khoảng đồng biến, khoảng nghịch biến của hàm số và lập bảng biến thiên của hàm số đó. Phương pháp giải: - Khoảng đồng biến: Khoảng mà đồ thị đi lên. - Khoảng nghịch biến: Khoảng mà đồ thị đi xuống. - Lập bảng biến thiên. Lời giải chi tiết: a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến. Bảng biến thiên:
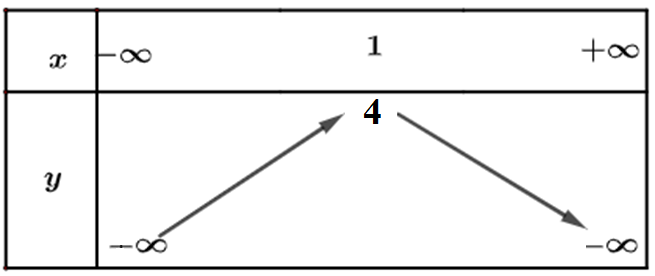
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến. Bảng biến thiên:
Luyện tập – vận dụng 3 Lập bảng biến thiên của mỗi hàm số sau: a) \(y = {x^2} - 3x + 4\) b) \(y = - 2{x^2} + 5\) Phương pháp giải: - Xác định hệ số a, b. - Tính \( - \frac{b}{{2a}}\). - Tìm khoảng đồng biến, nghịch biến. Lời giải chi tiết: a) Hệ số \(a = 1 > 0,b = - 3 \Rightarrow \frac{{ - b}}{{2a}} = \frac{3}{2}\) Vậy hàm số nghịch biến trên khoảng \(\left( { - \infty ;\frac{3}{2}} \right)\) và đồng biến trên \(\left( {\frac{3}{2}; + \infty } \right)\) b) Ta có \(a = - 2 < 0,b = 0\) \( \Rightarrow - \frac{b}{{2a}} = 0\) Vậy hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;0} \right)\) và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\)
|
















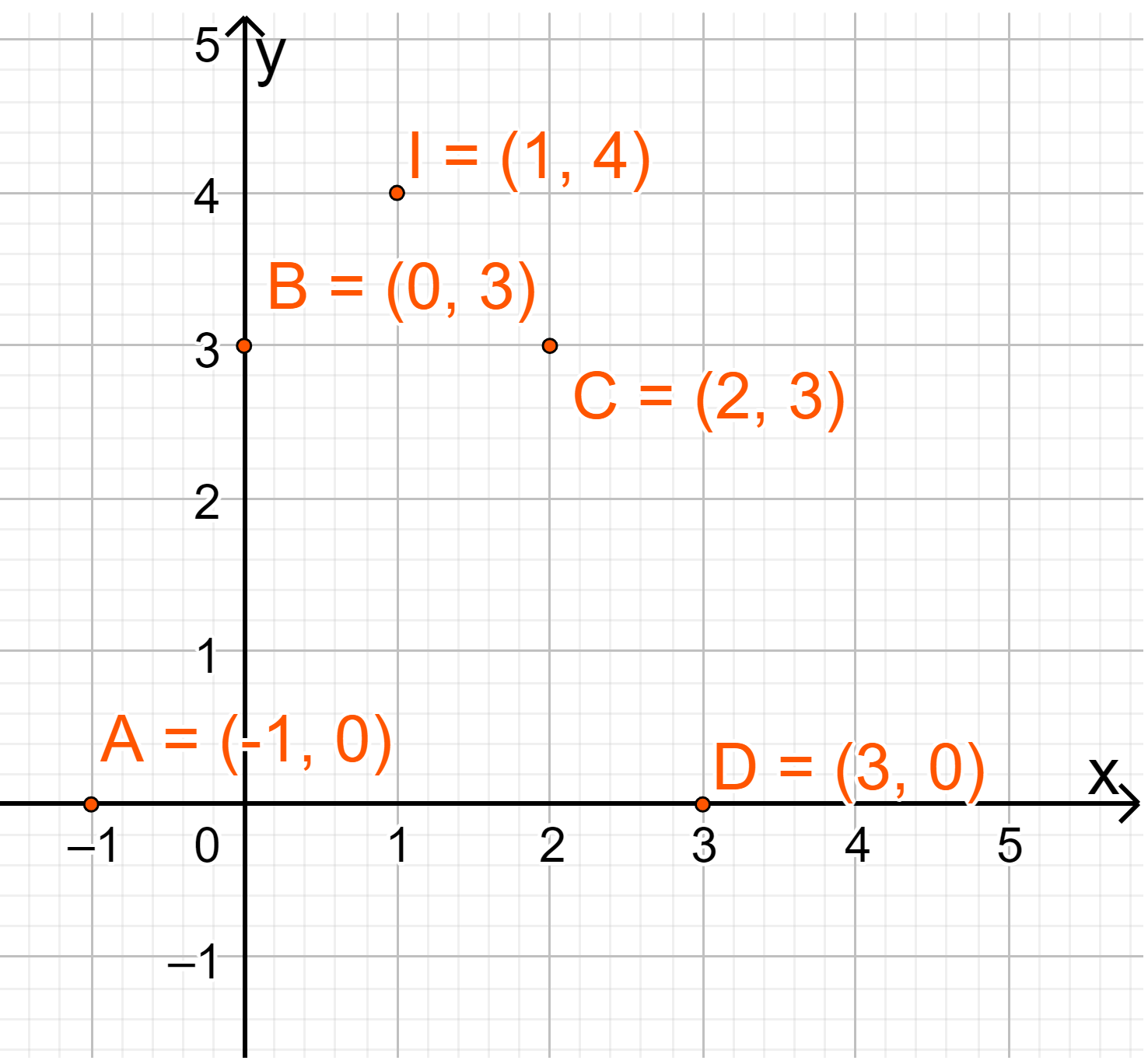







Danh sách bình luận