Giải bài 3 trang 43 SGK Toán 10 tập 1 – Cánh diềuVẽ đồ thị của mỗi hàm số sau: Quảng cáo
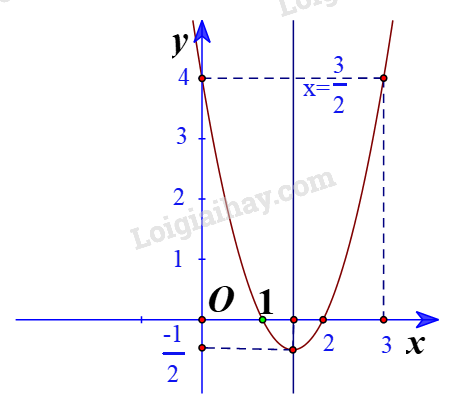
Đề bài Vẽ đồ thị của mỗi hàm số sau: a) \(y = 2{x^2} - 6x + 4\) b) \(y = - 3{x^2} - 6x - 3\) Phương pháp giải - Xem chi tiết Bước 1: Xác định tọa độ đỉnh \(\left( {\frac{{ - b}}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\) Bước 2: Vẽ trục đối xứng \(x = - \frac{b}{{2a}}\) Bước 3: Xác định một số điểm đặc biệt, chẳng hạn giao điểm với trục tung (0;c) và trục hoành (nếu có), điểm đối xứng với điểm (0;c) qua trục \(x = - \frac{b}{{2a}}\). Bước 4: Vẽ đường parabol đi qua các điểm đã xác định ta nhận được đồ thị hàm số \(y = a{x^2} + bx + c\). Lời giải chi tiết a) Hàm số có \(a = 2,b = - 6;c=4 \) \(\Rightarrow - \frac{b}{{2a}} = - \frac{{ - 6}}{{2.2}} = \frac{3}{2}; y\left( {\frac{3}{2}} \right) = 2{\left( {\frac{3}{2}} \right)^2} - 6.\frac{3}{2} + 4 = - \frac{1}{2} \) + Đồ thị hàm số có đỉnh \(I\left( {\frac{3}{2}; - \frac{1}{2}} \right)\) + Trục đối xứng là \(x = \frac{3}{2}\) + Giao điểm của parabol với trục tung là (0;4) + Giao điểm của parabol với trục hoành là (2;0) và (1;0) + Điểm đối xứng với điểm (0;4) qua trục đối xứng \(x = \frac{3}{2}\) là \(\left( {3;4} \right)\) Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
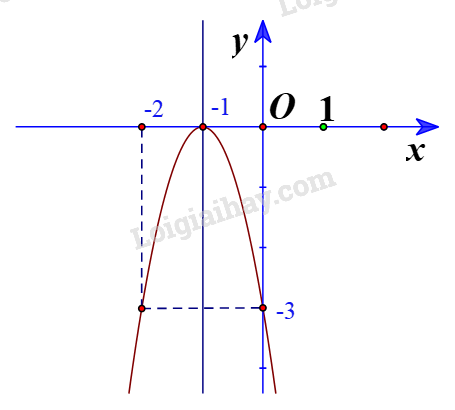
b) Hàm số có \(a = -3,b = - 6;c=-3 \) \(\Rightarrow - \frac{b}{{2a}} = - \frac{{ - 6}}{{2.(-3)}} =-1 ; y(-1) = - 3{(-1)^2} - 6.(-1) - 3 = 0 \) + Đồ thị hàm số có đỉnh \(I\left( { - 1;0} \right)\) + Trục đối xứng là \(x = - 1\) + Giao điểm của parabol với trục tung là (0;-3) + Giao điểm của parabol với trục hoành là \(I\left( { - 1;0} \right)\) + Điểm đối xứng với điểm (0;-3) qua trục đối xứng \(x = - 1\) là (-2;-3) Vẽ parabol đi qua các điểm được xác định ở trên, ta nhận được đồ thị hàm số:
 Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
