Giải mục II trang 34, 35 SGK Toán 10 tập 1 - Cánh diều

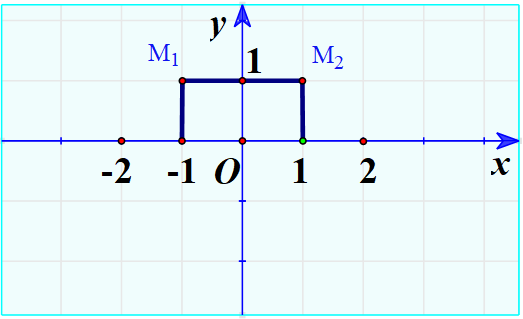
Hoạt động 4

Xét hàm số $y = f\left( x \right) = {x^2}$

a) Tính các giá trị ${y_1} = f\left( {{x_1}} \right),{y_2} = f\left( {{x_2}} \right)$ tương ứng với giá trị ${x_1} =  - 1;{x_2} = 1$.

b) Biểu diễn trong mặt phẳng tọa độ Oxy các điểm ${M_1}\left( {{x_1};{y_1}} \right),{M_2}\left( {{x_2};{y_2}} \right)$.

Phương pháp giải:

a) Thay ${x_1} =  - 1;{x_2} = 1$ vào tìm ${y_1} = f\left( {{x_1}} \right),{y_2} = f\left( {{x_2}} \right)$.

b) Xác định điểm và biểu diễn trên mặt phẳng.

Lời giải chi tiết:

a) Thay ${x_1} =  - 1;{x_2} = 1$ vào $y = {x^2}$ ta được:

${y_1} = f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1$

${y_2} = f\left( 1 \right) = {1^2} = 1$

b) Ta có ${x_1} =  - 1;{y_1} = 1 \Rightarrow {M_1}\left( { - 1;1} \right)$

Ta có: ${x_2} = 1;{y_2} = 1 \Rightarrow {M_2}\left( {1;1} \right)$

Biểu diễn trên mặt phẳng:

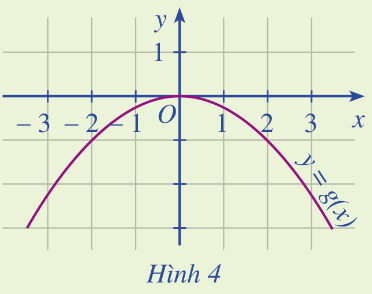
Luyện tập – vận dụng 4

Cho hàm số $y = \frac{1}{x}$ và ba điểm $M\left( { - 1; - 1} \right),N\left( {0;2} \right),P\left( {2;1} \right)$. Điểm nào thuộc đồ thị hàm số trên? Điểm nào không thuộc đồ thị hàm số trên?

Phương pháp giải:

- Tìm tập xác định của hàm số.

- Loại các điểm không thuộc tập xác định.

- Thay hoành độ x của các điểm còn lại, kết quả ra bằng tung độ thì điểm thuộc đồ thị, ngược lại thì không.

Lời giải chi tiết:

Tập xác định $D = \mathbb{R}\backslash \left\{ 0 \right\}$

Ta thấy ${x_N} = 0$=> Điểm N không thuộc đồ thị.

Thay ${x_M} =  - 1$ vào ta được: $y = \frac{1}{{ - 1}} =  - 1$=> Điểm M thuộc đồ thị.

Thay ${x_P} = 2$ vào ta được: $y = \frac{1}{2} \ne {y_P}$=> Điểm P không thuộc đồ thị.

Luyện tập – vận dụng 5

Dựa vào Hình 4, xác định $g\left( { - 2} \right),g\left( 0 \right),g\left( 2 \right)$.

Phương pháp giải:

- Xác định $x =  - 2,{\rm{ }}x = 0$ và $x = 2$ trên trục $Ox$.

- Kẻ đường thẳng vuông góc với $Ox$, cắt đồ thị tại điểm nào thì lại dóng sang tung độ tìm y.

Lời giải chi tiết:

+) Với $x =  - 2$, kẻ đường thẳng vuông góc với Ox thì cắt đồ thị tại điểm có tung độ bằng $y =  - 1$

+) Với $x = 0 \Rightarrow y = 0$

+) Với $x = 2 \Rightarrow y =  - 1$