Giải mục 2 trang 79, 80, 81 SGK Toán 7 tập 2 - Kết nối tri thứcVẽ tam giác ABC và 3 đường cao của nó. Quan sát hình và cho biết, ba đường cao đó có cùng đi qua một điểm hay không ? Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
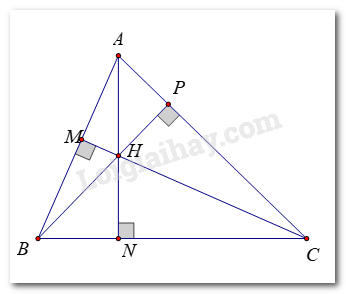
Câu hỏi Mỗi tam giác có mấy đường cao? Phương pháp giải: Đường cao là đoạn thẳng đi qua đỉnh và vuông góc với cạnh đối diện. Lời giải chi tiết: Ứng với 1 cạnh của tam giác, ta có 1 đường cao Vậy mỗi tam giác có 3 đường cao. HĐ 3 Vẽ tam giác ABC và 3 đường cao của nó. Quan sát hình và cho biết, ba đường cao đó có cùng đi qua một điểm hay không ? Phương pháp giải: Đường cao của một tam giác là đoạn thẳng kẻ từ một đỉnh và vuông góc với cạnh đối diện Lời giải chi tiết:
Ba đường cao AN, BP, CM cùng đi qua điểm H. Luyện tập 2 a) Chứng minh trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó. b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác. Phương pháp giải: a) Chứng minh A thuộc đường trung trực BC nên AD là đường cao. Chứng minh: \(\Delta ABD = \Delta ACD\) từ đó suy ra AD là phân giác góc A b) Điểm cách đều ba đỉnh là giao của ba đường trung trực trong tam giác GA = GB = GC Sử dụng kết quả ý a, chứng minh G là giao điểm ba đường phân giác trong tam giác ABC Lời giải chi tiết:
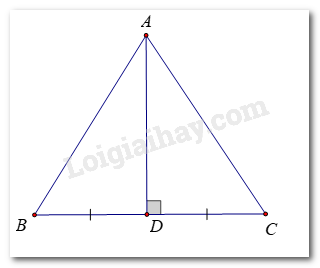
a) Kẻ đường trung trực của đoạn thẳng BC, cắt BC tại D Ta có: Tam giác ABC cân nên AB = AC \( \Rightarrow A\)thuộc đường trung trực của cạnh BC (t/c) \( \Rightarrow AD\)là đường trung trực của BC. Xét \(\Delta ABD\)và \(\Delta ACD\)có: AB = AC (gt) BD = CD (gt) AD: cạnh chung \( \Rightarrow \Delta ABD = \Delta ACD\left( {c - c - c} \right)\) \( \Rightarrow \widehat {BAD} = \widehat {CAD}\) \( \Rightarrow \)AD là tia phân giác góc BAC. b)
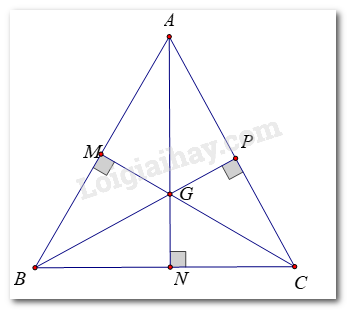
Ta có: Điểm cách đều ba đỉnh của tam giác là giao điểm ba đường trung trực của tam giác đó. Tam giác ABC đều nên AB = BC = CA Tam giác ABC cân tại A có AN là đường trung tuyến \( \Rightarrow \) AN là đường phân giác xuất phát từ đỉnh A (cm ở ý a) Tương tự: BP, CM lần lượt là đường phân giác xuất phát từ B và C của tam giác ABC Mà AN cắt BP tại G \( \Rightarrow G\) là giao điểm ba đường phân giác của tam giác ABC \( \Rightarrow G\) cách đều ba cạnh của tam giác ABC (Tính chất)
|




















Danh sách bình luận