Giải mục 2 trang 37,38 SGK Toán 7 tập 2 - Kết nối tri thứcTính (2x – 3) . (x^2 – 5x + 1) bằng cách thực hiện các bước sau: Bước 1: Nhân 2x với đa thức x^2 – 5x + 1 Bước 2: Nhân (-3) với đa thức x^2 – 5x + 1 Bước 3: Cộng các đa thức thu được ở hai bước trên và thu gọn Kết quả thu được là tích của đa thức 2x – 3 với đa thức x^2 – 5x + 1 Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
2. Nhân đa thức với đa thức HĐ 3 Tính (2x – 3) . (x2 – 5x + 1) bằng cách thực hiện các bước sau: Bước 1: Nhân 2x với đa thức x2 – 5x + 1 Bước 2: Nhân (-3) với đa thức x2 – 5x + 1 Bước 3: Cộng các đa thức thu được ở hai bước trên và thu gọn Kết quả thu được là tích của đa thức 2x – 3 với đa thức x2 – 5x + 1 Phương pháp giải: Thực hiện theo 3 bước trên Lời giải chi tiết: Ta có: (2x – 3) . (x2 – 5x + 1) = 2x. (x2 – 5x + 1) + (-3). (x2 – 5x + 1) = 2x . x2 + 2x . (-5x) + 2x . 1 + (-3).x2 + (-3).(-5x) + (-3). 1 = 2x3 + (-10x2 ) + 2x + (-3x2) + 15x + (-3) = 2x3 + (-10x2 + -3x2) + (2x + 15x) + (-3) Luyện tập 2 Tính (x3 – 2x2 + x – 1)(3x – 2). Trình bày lời giải theo 2 cách. Phương pháp giải: Cách 1: Muốn nhân một đa thức với một đa thức, ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các tích với nhau Cách 2: Đặt tính nhân: + Nhân lần lượt mỗi hạng tử ở dòng dưới với đa thức ở dòng trên và viết kết quả trong một dòng riêng. + Viết các dòng sao cho các hạng tử cùng bậc thẳng cột với nhau để thực hiện phép cộng theo cột. Lời giải chi tiết: Cách 1: (x3 – 2x2 + x – 1) (3x – 2) = x3 . (3x – 2) + (-2x2) .(3x – 2) + x .(3x – 2) + (-1) . (3x – 2) = x3 . 3x + x3 . (-2) + (-2x2). 3x + (-2x2) . (-2) + x . 3x + x. (-2) + (-1). 3x + (-1). (-2) = 3x4 – 2x3 – 6x3 + 4x2 + 3x2 – 2x – 3x + 2 = 3x4 + (-2x3 -6x3) + (4x2 + 3x2 ) + (-2x – 3x) + 2 = x4 + (-8x3) + 7x2 + (-5x) + 2 = x4 – 8x3 +7x2 – 5x + 2 Cách 2: Vận dụng 2 Rút gọn biểu thức (x – 2) . (2x3 – x2 + 1) + (x – 2) x2(1 – 2x) Phương pháp giải: Sử dụng tính chất phân phối của phép nhân đối với phép cộng Lời giải chi tiết: (x – 2) . (2x3 – x2 + 1) + (x – 2) x2(1 – 2x) = (x – 2). [(2x3 – x2 + 1) + x2(1 – 2x)] = (x – 2). [2x3 – x2 + 1 + x2 . 1 + x2 . (-2x)] = (x – 2) . (2x3 – x2 + 1 + x2 – 2x3) = (x – 2) .1 = x – 2 Vận dụng 3 Trở lại bài toán đoán tuổi, để giải thích bí mật trong bài toán đoán tuổi của anh Pi, em hãy thực hiện các yêu cầu sau: * Gọi x là tuổi cần đoán. Tìm đa thức ( biến x) biểu thị kết quả thứ nhất và kết quả thứ hai * Tìm đa thức biểu thị kết quả cuối cùng. Từ đó hãy nêu cách tìm x. Phương pháp giải: Tìm đa thức biểu thị từng kết quả thứ nhất và thứ hai. Lấy kết quả thứ nhất trừ đi kết quả thứ hai. Lời giải chi tiết: Đa thức biểu thị kết quả thứ nhất: K = (x + 1)2 Đa thức biểu thị kết quả thứ hai: H = (x – 1)2 Đa thức biểu thị kết quả cuối cùng: Q = K – H = (x + 1)2 - (x – 1)2 = (x+1).(x+1) - (x – 1). (x – 1) = x.(x+1) + 1.(x+1) - x(x-1) + (-1). (x-1) = x.x + x.1 + 1.x + 1.1 –[ x.x – x .1 + (-1).x + (-1) . (-1)] = x2 + x + x + 1 – (x2 – x – x + 1) = x2 + x + x + 1 – x2 + x + x – 1 = (x2 - x2 ) + (x+x+x+x) + (1- 1) = 4x Để tìm x, ta lấy kết quả cuối cùng chia cho 4
|














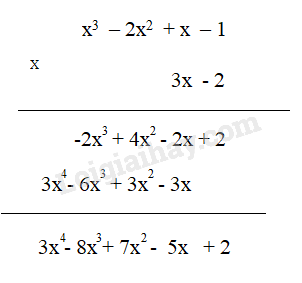






Danh sách bình luận