Giải bài 9.38 trang 84 SGK Toán 7 tập 2 - Kết nối tri thức

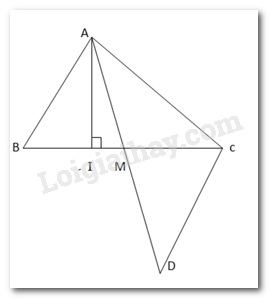
Đề bài

Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng

a) $AI < \dfrac{1}{2}\left( {AB + AC} \right)$

b) $AM < \dfrac{1}{2}\left( {AB + AC} \right)$

Lời giải chi tiết

a)

AI là đường vuông góc kẻ từ A xuống đoạn thẳng BC.

$\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}AI < AB\\AI < AC\end{array} \right.\\ \Rightarrow 2AI < AB + AC\\ \Rightarrow AI < \dfrac{1}{2}\left( {AB + AC} \right)\end{array}$ (đường vuông góc nhỏ hơn đường xiên)

b)

Lấy D sao cho M là trung điểm của AD

Xét $\Delta ABM$ và $DCM$ có

AM = DM ( do M là trung điểm của AD)

BM = CM ( do M là trung điểm của BC)

$\widehat {AMB} = \widehat {CMD}$( 2 góc đối đỉnh)

$\Rightarrow \Delta ABM = \Delta DCM\left( {c - g - c} \right)$

$\Rightarrow AB = CD$(2 cạnh tương ứng)

Xét  $\Delta ADC$ ta có: AD < AC + CD (bất đẳng thức tam giác)

$\Rightarrow$   2AM < AC + AB

$\Rightarrow$   AM < $\dfrac{1}{2}$(AB + AC)