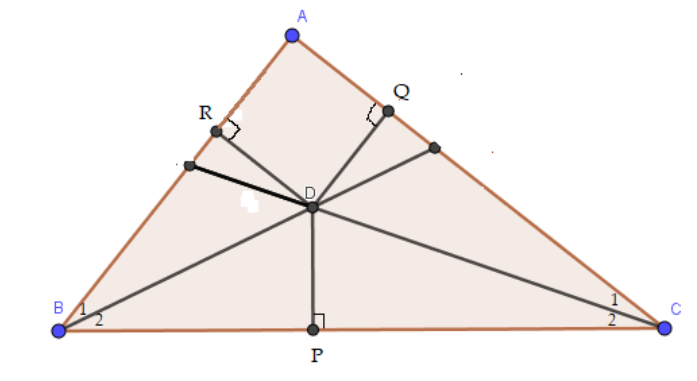
Giải bài 9.25 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức

Đề bài

Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB.

a) Hãy giải thích tại sao DP = DR.

b) Hãy giải thích tại sao DP = DQ.

c) Từ câu a và b suy ra DR = DQ. Tại sao D nằm trên tia phân giác của góc A? ( Đây là một cách chứng minh định lí 2)

Lời giải chi tiết

a) Vì BD là tia phân giác của góc ABC nên \(\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}\)

Vì CD là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}\)

Xét \(\Delta BDP\) vuông tại P và \(\Delta BDR\) vuông tại R, ta có:

 \(\widehat {{B_2}} = \widehat {{B_1}}\)

BD chung

\( \Rightarrow \Delta BDP = \Delta BDR\) ( cạnh huyền – góc nhọn)

\( \Rightarrow \) DP = DR ( 2 cạnh tương ứng) (1)

b) Xét \(\Delta CDP\) vuông tại P và \(\Delta CDQ\) vuông tại Q, ta có:

 \(\widehat {{C_2}} = \widehat {{C_1}}\)

CD chung

\( \Rightarrow \Delta CDP = \Delta CDQ\) ( cạnh huyền – góc nhọn)

\( \Rightarrow \) DP = DQ ( 2 cạnh tương ứng) (2)

c) Từ (1) và (2), ta được: DR = DQ ( cùng bằng DP).

D nằm trên tia phân giác của góc A do D cách đều AB và AC.