Giải bài 9.20 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức

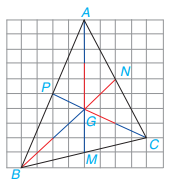
Đề bài

Cho tam giác ABC với hai đường trung tuyến BN, CP và trọng tâm G. Hãy tìm số thích hợp vào chỗ chấm hỏi để được các đẳng thức:

BG = ? BN, CG = ? CP;

BG = ? GN, CG = ? GP.

Lời giải chi tiết

Vì G là trọng tâm của $\Delta ABC$ nên $BG = \dfrac{2}{3}BN,CG = \dfrac{2}{3}CP$

Ta có: $GN = BN – BG = BN - \dfrac{2}{3}BN = \dfrac{1}{3}BN;\\ GP = CP – CG = CP - \dfrac{2}{3}CP = \dfrac{1}{3}CP$

Do đó, $BN = 3. GN ; CP = 3. GP$

Như vậy, $BG = \dfrac{2}{3}BN = \dfrac{2}{3}.3.GN = 2GN;\\CG = \dfrac{2}{3}CP = \dfrac{2}{3}.3.GP = 2GP$

Vậy $BG = \dfrac{2}{3}BN,CG = \dfrac{2}{3}CP$;

$BG = 2GN; CG = 2GP$.