Giải bài 9.24 trang 76 SGK Toán 7 tập 2 - Kết nối tri thức

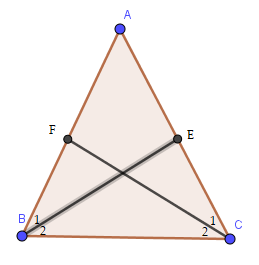
Đề bài

Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF.

Lời giải chi tiết

Vì tam giác ABC cân tại A nên AB = AC; $\widehat {ABC} = \widehat {ACB}$ ( tính chất)

Vì BE là là tia phân giác của góc ABC nên $\widehat {{B_1}} = \widehat {{B_2}} = \dfrac{1}{2}.\widehat {ABC}$

Vì CF là tia phân giác của góc ACB nên $\widehat {{C_1}} = \widehat {{C_2}} = \dfrac{1}{2}.\widehat {ACB}$

Do đó, $\widehat {{B_1}} = \widehat {{C_1}}$

Xét $\Delta ABE$ và $\Delta ACF$, ta có:

$\widehat A$ chung

AB = AC

$\widehat {{B_1}} = \widehat {{C_1}}$

$\Rightarrow \Delta ABE = \Delta ACF\left( {g.c.g} \right)$

$\Rightarrow$BE = CF ( 2 cạnh tương ứng)