Bài 51 trang 166 SBT toán 8 tập 1

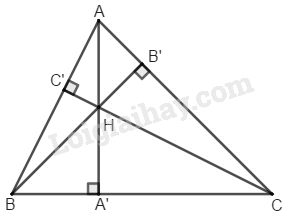
Đề bài

Cho tam giác \(ABC\) với ba đường cao \(AA’,\, BB’,\ CC’.\) Gọi \(H\) là trực tâm của tam giác đó.

Chứng minh rằng: \(\eqalign{{HA'} \over {AA'}} + \eqalign{{HB'} \over {BB'}} +\eqalign {{HC'} \over {CC'}} = 1\)

Lời giải chi tiết

\(\eqalign{  & {S_{HBC}} + {S_{HAC}} + {S_{HAB}} = {S_{ABC}}  \cr  &  \Rightarrow {{{S_{HBC}}} \over {{S_{ABC}}}} + {{{S_{HABC}}} \over {{S_{ABC}}}} + {{{S_{HAB}}} \over {{S_{ABC}}}} = 1 \cr} \)

\( \Rightarrow \dfrac{{\dfrac{1}{2}HA'.BC}}{{\dfrac{1}{2}AA'.BC}} + \dfrac{{\dfrac{1}{2}HB'.AC}}{{\dfrac{1}{2}BB'.AC}} + \dfrac{{\dfrac{1}{2}HC'.AB}}{{\dfrac{1}{2}CC'.AB}} = 1\)

\( \Rightarrow \eqalign{{HA'} \over {AA'}} + \eqalign{{HB'} \over {BB'}} +\eqalign{{HC'} \over {CC'}} = 1\)

Loigiaihay.com