Giải bài 4.24 trang 84 SGK Toán 7 tập 1 - Kết nối tri thức

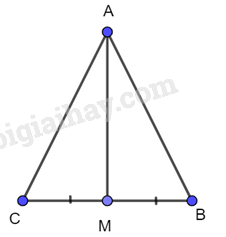
Đề bài

Cho tam giác ABC cân tại A và M là trung điểm của đoạn thẳng BC. Chứng minh AM vuông góc với BC và AM là tia phân giác của góc BAC.

Lời giải chi tiết

Xét 2 tam giác AMB và AMC có:

AM chung

AB=AC (do tam giác ABC cân tại A)

MB=MC (gt)

Do đó \(\Delta AMB=\Delta AMC\) (c.c.c)

Suy ra \(\widehat {BAM} = \widehat {CAM}\) (2 góc tương ứng).

Mà tia AM nằm trong góc BAC nên AM là phân giác của góc BAC

Mặt khác: Do \(\Delta AMB=\Delta AMC\) nên \(\widehat {AMB} = \widehat {AMC}\) (2 góc tương ứng) mà \(\widehat {AMB} + \widehat {AMC} = {180^o}\) (2 góc kề bù)

Nên \(\widehat {AMB} = \widehat {AMC} = {90^o}\).

Vậy AM vuông góc với BC.