Giải bài 4.10 trang 69 SGK Toán 7 tập 1 - Kết nối tri thức

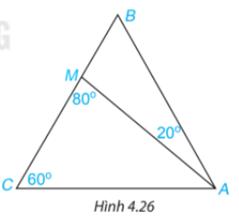
Đề bài

Cho tam giác ABC có \(\widehat {BCA} = {60^o}\) và điểm M nằm trên cạnh BC sao cho \(\widehat {BAM} = {20^\circ },\widehat {AMC} = {80^\circ }({\rm{H}}.4.26).\) Tính số đo các góc AMB, ABC, BAC.

Lời giải chi tiết

Ta có:

\(\widehat {AMB} + \widehat {AMC} = {180^o}\)( 2 góc kề bù)

\(\begin{array}{l} \Rightarrow \widehat {AMB} + {80^o} = {180^o}\\ \Rightarrow \widehat {AMB} = {100^o}\end{array}\)

Áp dụng định lí tổng ba góc trong một tam giác:

+) Trong tam giác AMB có:

\(\begin{array}{l}\widehat {ABC} + \widehat {MAB} + \widehat {AMB} = {180^O}\\ \Rightarrow \widehat {ABC} + {20^o} + {100^o} = {180^O}\\ \Rightarrow \widehat {ABC} = {60^o}\end{array}\)

+) Trong tam giác ABC có:
\(\begin{array}{l}\widehat {BAC} + \widehat {ACB} + \widehat {CBA} = {180^o}\\ \Rightarrow \widehat {BAC} + {60^o} + {60^o} = {180^o}\\ \Rightarrow \widehat {BAC} = {60^o}\end{array}\)