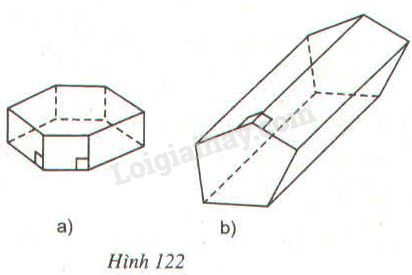
Bài 32 trang 140 SBT toán 8 tập 2

LG a

Viết các công thức liên hệ giữa \(n, m, d, c\).

Phương pháp giải:

Sử dụng: Công thức liên hệ giữa \(n, m, d, c\):

\(m = n + 2\); \(d = 2n\); \(c = 3n\).

Trong đó: \(n\) là số cạnh của một đáy

               \(m\) là số mặt

               \(d\) là số đỉnh

               \(c\) là số cạnh.

Lời giải chi tiết:

a) Công thức liên hệ giữa \(n, m, d, c\): 

\(m = n + 2\);

\(d = 2n\);

\(c = 3n\).

LG b

Hình lăng trụ đứng có \(20\) đỉnh thì có bao nhiêu mặt, bao nhiêu cạnh?

Phương pháp giải:

Sử dụng: Công thức liên hệ giữa \(n, m, d, c\):

\(m = n + 2\); \(d = 2n\); \(c = 3n\).

Trong đó: \(n\) là số cạnh của một đáy

               \(m\) là số mặt

               \(d\) là số đỉnh

               \(c\) là số cạnh.

Lời giải chi tiết:

Số cạnh của một đáy là:

\(\displaystyle n = {d \over 2} = {{20} \over 2} = 10\) (cạnh)

Hình lăng trụ có \(20\) đỉnh, thì:

Số mặt là: \(m = n + 2 = 10 + 2 = 12\) (mặt)

Số cạnh là: \(c = 3n = 3.10 = 30\) (cạnh)

LG c

Có thể làm được một hình lăng trụ đứng có \(15\) đỉnh hay không?

Phương pháp giải:

Sử dụng: Công thức liên hệ giữa \(n, m, d, c\):

\(m = n + 2\); \(d = 2n\); \(c = 3n\).

Trong đó: \(n\) là số cạnh của một đáy

               \(m\) là số mặt

               \(d\) là số đỉnh

               \(c\) là số cạnh.

Lời giải chi tiết:

Không thể làm một hình lăng trụ đứng có \(15\) đỉnh vì \(d = 2n\) (số đỉnh của lăng trụ là một số chẵn).

Loigiaihay.com