Bài 36 trang 142 SBT toán 8 tập 2

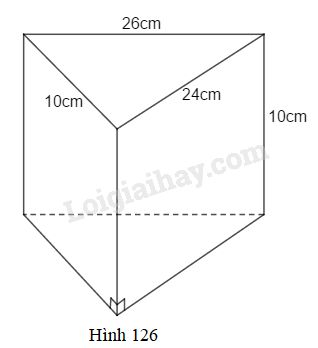
Đề bài

Một cái chặn giấy bằng thủy tinh hình lăng trụ đứng có các kích thước cho ở hình 126. Diện tích toàn phần của nó là:

A. \(840c{m^2}\)                                     B. \(620c{m^2}\)

C. \(670c{m^2}\)                       D. \(580c{m^2}\)

E. \(600c{m^{2}}\)  

Hãy chọn kết quả đúng.

Lời giải chi tiết

Ta có: \({10^2} + {24^2} = {26^2}\)

Theo định lí Pytago đảo thì tam giác đáy của hình lăng trụ là tam giác vuông có cạnh huyền là \(26cm\) và hai cạnh góc vuông là \(10cm;24cm\).

Diện tích xung quanh hình lăng trụ là:

\({S_{xq}} = (10+ 24 + 26).10 = 600(c{m^2})\)

Diện tích mặt đáy hình lăng trụ là:

\(S_đ = \dfrac{1}{2}.10.24 = 120\,\left( {cm^2} \right)\)

Diện tích toàn phần hình lăng trụ là:

\({S_{TP}} = {S_{xq}} + 2.{S_đ} = 600 + 2.120 \)\(\,= 840\,\left( {c{m^2}} \right)\)

Chọn A.

Loigiaihay.com