Bài 2.9 phần bài tập bổ sung trang 168 SBT toán 8 tập 1Giải bài 2.9 phần bài tập bổ sung trang 168 sách bài tập toán 8. Cho hình bs.32 (tam giác MNP vuông tại đỉnh M và NRQP, PUTM, MKHN đều là hình vuông, còn S1, S2, S3 tương ứng là diện tích của mỗi hình... Quảng cáo
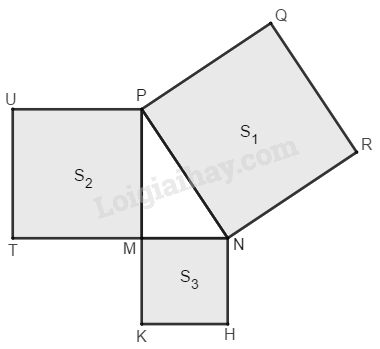
Đề bài Cho hình bs.32 (tam giác \(MNP\) vuông tại đỉnh \(M\) và \(NRQP,\, PUTM,\, MKHN\) đều là hình vuông, còn \(S_1,\, S_2,\,S_3\) tương ứng là diện tích của mỗi hình. Quan hệ nào sau đây là đúng? (A) \(S_3+S_2=S_1\) (B) \({S_3}^2+{S_2}^2={S_1}^2\) (C) \(S_3+S_2>S_1\) (D) \({S_3}^2+{S_2}^2<{S_1}^2\)
Phương pháp giải - Xem chi tiết Áp dụng định lý Pi - ta - go: Trong tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông. Diện tích hình vuông cạnh \(a\) bằng \(a^2\) Lời giải chi tiết Gọi độ dài của \(PM ,\,MN, \,PN\) lần lượt là \(a,\, b,\, c.\) Tam giác \(PMN\) vuông tại \(M,\) theo định lý Pi – ta - go ta có: \({a^2} + {b^2} = {c^2}\) Do các tứ giác \( PUTM,\ NRQP,\, MKHN\) đều là hình vuông và có độ dài các cạnh lần lượt là \(a, \,b,\,c\) nên diện tích của chúng tương ứng là: \({a^2},{b^2},{c^2}\) Như vậy: \({S_1} = {c^2},{S_2} = {a^2},{S_3} = {b^2}\) mà \({a^2} + {b^2} = {c^2}\) Nên ta có hệ thức: \({S_2} + {S_3} = {S_1}\) Chọn (A) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
