Bài 137 trang 97 SBT Toán 8 tập 1

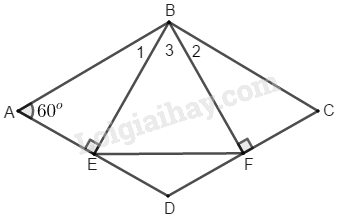
Đề bài

Hình thoi \(ABCD\) có \(\widehat A = {60^0}\). Kẻ hai đường cao \(BE,\, BF.\) Tam giác \(BEF\) là tam giác gì ? Vì sao ?

Lời giải chi tiết

Xét hai tam giác vuông \(BEA\) và \(BFC:\)

\(\widehat {BEA} = \widehat {BFC} = {90^0}\)

\(\widehat A = \widehat C\) (tính chất hình thoi ABCD)

\(BA = BC\) (vì ABCD là hình thoi)

Do đó: \(∆ BEA = ∆ BFC\) (cạnh huyền, góc nhọn)

\(⇒ BE = BF\) (hai cạnh tương ứng) \(⇒ ∆BEF\) cân tại \(B\)

\( \Rightarrow {\widehat B_1} = {\widehat B_2}\) (hai góc tương ứng)

Trong tam giác vuông \(BEA\) ta có:

\(\widehat A + {\widehat B_1} = {90^0}\)

\( \Rightarrow {\widehat B_1} = {90^0} - \widehat A\)\( = {90^0} - {60^0} = {30^0} \)\( \Rightarrow {\widehat B_2} = {\widehat B_1} = {30^0} \)

\( \widehat A + \widehat {ABC} = {180^0}\) (hai góc trong cùng phía bù nhau)

\(\Rightarrow \widehat {ABC} = {180^0} - \widehat A\)\( = {180^0} - {60^0} = {120^0}\)

\( \widehat {ABC} = {\widehat B_1} + {\widehat B_2} + {\widehat B_3}\)\(  \Rightarrow {\widehat B_3} = \widehat {ABC} - \left( {{{\widehat B}_1} + {{\widehat B}_2}} \right)\)\( = {120^0} - \left( {{{30}^0} + {{30}^0}} \right) = {60^0} \)

Vậy \(∆ BEF\) cân có \(\widehat {EBF}=60^0\) nên nó là tam giác đều.

Loigiaihay.com