Bài 102 trang 92 SBT toán 8 tập 1Giải bài 102 trang 92 sách bài tập toán 8. Cho tam giác ABC có trực tâm H. Gọi M là trung điểm của BC, K là điểm đối xứng với H qua M. Tính số đo góc ABK, ACK. Quảng cáo
Đề bài Cho tam giác \(ABC\) có trực tâm \(H.\) Gọi \(M\) là trung điểm của \(BC,\) \(K\) là điểm đối xứng với \(H\) qua \(M.\) Tính số đo góc \(ABK,\) \(ACK.\) Phương pháp giải - Xem chi tiết Sử dụng kiến thức: +) Hai điểm gọi là đối xứng với nhau qua \(O\) nếu \(O\) là trung điểm của đoạn thẳng nối hai điểm đó +) Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành. Lời giải chi tiết
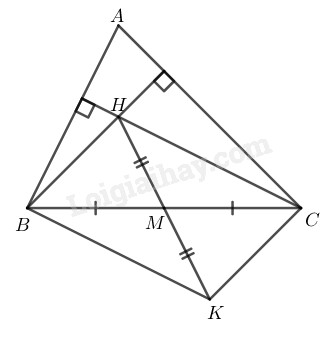
Ta có \(K\) là điểm đối xứng của \(H\) qua tâm \(M\) nên \(MK = MH\) Xét tứ giác \(BHCK\) ta có: \(BM = MC\) (do M là trung điểm của BC) \(MK = MH\) (chứng minh trên) Suy ra: Tứ giác \(BHCK\) là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm mỗi đường) Suy ra: \(KB // CH, KC // BH\) Vì H là trực tâm tam giác ABC nên \( CH ⊥ AB\) và \(BH ⊥ AC\) Suy ra: \(KB ⊥ AB\) nên \(\widehat {KBA} = {90^0}\) \(CK ⊥ AC \) nên \(\widehat {KCA} = {90^0}\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
