Đề kiểm tra học kì 1 Toán 9 - Đề số 28

Đề bài

PHẦN TRẮC NGHIỆM (3,0 điểm)

Câu 1: Hệ số góc của đường thẳng \(2x - y = 4\)là

A. \( - 2.\)

B. \(1.\)

C. \(\frac{1}{2}.\)

D. \(2.\)

Câu 2: Đường thẳng \(y =  - 2x + 3\) có tung độ gốc là

A. \( - 2.\)

B. \( - 3.\)

C. \(3.\)

D. \(2.\)

Câu 3: Đường thẳng nào sau đây không song song với đường thẳng \(y = 5 - 3x\)?

A. \(y = 3x - 5.\)

B. \(y =  - 3x + 2.\)

C. \(y =  - 3x + 7.\)

D. \(y = 5 + 3(1 - x).\)

Câu 4: Công thức nghiệm tổng quát của phương trình \( - x + 2y = 0\) là

A. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 2x\end{array} \right.\)

B. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = \frac{x}{2}\end{array} \right.\)

C. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = \frac{{ - x}}{2}\end{array} \right.\)

D. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y =  - 2x\end{array} \right.\)

Câu 5: Rút gọn biểu thức \(2021\sqrt {{x^2}y}  + x\sqrt y \) với \(x < 0\) và \(y > 0\) ta được kết quả là:

A. \( - 2022x\sqrt y .\)

B. \( - 2020\sqrt {{x^2}y} .\)

C. \(2022x\sqrt y .\)

D. \( - 2020x\sqrt y .\)

Câu 6: Cho hai đường tròn \((O;5cm)\) và \((O';3cm)\). Nếu \(OO' = 2cm\) thì vị trí tương đối của hai đường tròn đó là

A. tiếp xúc trong.

B. tiếp xúc ngoài.

C. không giao nhau.

D. cắt nhau.

Câu 7: Tính  \(\sqrt[3]{8} - \sqrt[3]{{ - 27}}\) ta được kết quả là

A. -19.

B. 5.

C. -1.

D. 1.

Câu 8: Các giá trị không âm của \(x\) để \(\sqrt x  < \sqrt 3 \) là

A. \(x > 3.\)

B. \(x = 3.\)

C. \(0 \le x < 3.\)

D. \(x < 3.\)

Câu 9: Cho tam giác \(DEF\)vuông tại \(D\) có \(DE = 1cm,\,DF = \sqrt 3 cm\). Trong các khẳng định sau khẳng định nào đúng?

A. \(\sin F = \frac{1}{2}.\)

B. \(\tan F = \sqrt 3 .\)

C. \(\sin E = \frac{1}{2}.\)

D. \(\cos E = \frac{{\sqrt 3 }}{2}.\)

Câu 10: Cho tam giác ABC vuông tại A, đường cao\(AH(H \in BC).\) Biết \(HB = 3cm;AH = 4cm.\) Độ dài \(HC\) là

A. \(\frac{{16}}{3}cm.\)

B. \(\frac{7}{3}cm.\)

C. \(3cm.\)

D. \(\frac{{25}}{3}cm.\)

Câu 11: Cho \(a \le 5\), giá trị của biểu thức \(\sqrt {{a^2} - 10a + 25}  - 2a + 3\) bằng

A. \(8 + 3a.\)

B. \(3a - 8.\)

C. \(8 - 3a.\)

D. \(7 - 3a.\)

Câu 12: Cho tam giác ABC vuông tại A có BC = 2AB. Khi đó số đo góc B bằng

A. \({60^0}.\)

B. \({45^0}.\)

C. \({30^0}.\)

D. \({40^0}.\)

Câu 13: Cho đường tròn \((O;6cm),\) có dây cung MN cách tâm O một khoảng bằng 3cm. Khi đó độ dài dây MN bằng

A. \(\sqrt 3 cm.\)

B. \(6\sqrt 3 cm.\)

C. \(3cm.\)

D. \(3\sqrt 3 cm.\)

Câu 14: Tất cả các giá trị của \(x\) để biểu thức \(\sqrt {1 - x} \) có nghĩa là

A. \(x \ge 0\).

B. \(x > 1\).

C. \(x \ge  - 1\).

D. \(x \le 1\).

Câu 15: Hàm số \(y = ({m^2} - 1)x + m\)(\(m\) là tham số) là hàm số bậc nhất khi

A. \(m \ne  \pm 1{\rm{ }}{\rm{.}}\)

B. \(m \ne 0.\)

C. \(m = 1.\)

D. \(m \ne 1.\)

PHẦN TỰ LUẬN (7,0 điểm).

Bài 1: (3,0 điểm)

1) Tính giá trị của biểu thức \(\sqrt {{{\left( {\sqrt 2  - 1} \right)}^2}}  - \sqrt 2 .\)

2) Hàm số \(y = \left( {2 - \sqrt 5 } \right)x - 2\)đồng biến hay nghịch biến trên \(\mathbb{R}\)? Vì sao?

3) Tìm các giá trị của tham số \(m\)để đường thẳng \((d):y = (m - 3)x + 2\) đi qua điểm \(A\left( { - 1;5} \right)\).

Bài 2: (1,5 điểm)

Cho biểu thức \(A = \frac{{x + 1}}{{x - 1}} - \frac{1}{{\sqrt x  + 1}} - \frac{1}{{\sqrt x  - 1}}\) với \(x \ge 0\), \(x \ne 1\).

1) Rút gọn biểu thức \(A.\)

2) Tính giá trị của biểu thức \(A\)  tại \(x = 4 + 2\sqrt 3 .\)

Bài 3: (2,0 điểm)

Cho đường tròn (O) đường kính AB, C là điểm bất kỳ trên đường tròn (C khác A, B). Gọi H là hình chiếu của C trên AB, M là trung điểm của CH. Kẻ tia MK vuông góc với CO (K thuộc OC) cắt đường tròn (O) tại E. Kẻ đường kính CI của đường tròn (O) . Chứng minh:

1) \(CE \bot EI.\)

2) Tam giác \(CEH\)cân.

Bài 4: (0,5 điểm) Cho  các số thực \(x,\,y\)thỏa mãn \(\left( {x + \sqrt {2021 + {x^2}} } \right)\left( {y + \sqrt {2021 + {y^2}} } \right) = 2021\). Tính giá trị của biểu thức: \(M = {x^{2021}} + {y^{2021}} + 2022\).

-------- Hết --------

Lời giải

Phần trắc nghiệm

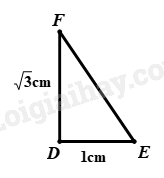
Câu 1: Hệ số góc của đường thẳng \(2x - y = 4\)là

A. \( - 2.\)

B. \(1.\)

C. \(\frac{1}{2}.\)

D. \(2.\)

Phương pháp giải

Đường thẳng \(y = ax + b\) có hệ số góc là \(a\)

Lời giải

Ta có: \(2x - y = 4 \Rightarrow y = 2x - 4\)

Hệ số góc của đường thẳng \(2x - y = 4\) là \(2\)

Đáp án D.

Câu 2: Đường thẳng \(y =  - 2x + 3\) có tung độ gốc là

A. \( - 2.\)

B. \( - 3.\)

C. \(3.\)

D. \(2.\)

Phương pháp giải

Tung độ gốc là điểm mà tại đó, đường thẳng cắt trục tung

Lời giải

Đường thẳng \(y =  - 2x + 3\) có tung độ gốc là \(3\)

Đáp án C.

Câu 3: Đường thẳng nào sau đây không song song với đường thẳng \(y = 5 - 3x\)?

A. \(y = 3x - 5.\)

B. \(y =  - 3x + 2.\)

C. \(y =  - 3x + 7.\)

D. \(y = 5 + 3(1 - x).\)

Phương pháp giải

Đường thẳng \(\left( d \right):y = ax + b\) song song với đường thẳng \(\left( {d'} \right):y = a'x + b'\) khi và chỉ khi \(\left\{ \begin{array}{l}a = a'\\b \ne b'\end{array} \right.\).

Lời giải

Ta có: \(\left\{ \begin{array}{l}3 \ne  - 3\\ - 5 \ne 5\end{array} \right.\) do đó, đường thẳng \(y = 5 - 3x\) cắt đường thẳng \(y = 3x - 5\)

Đáp án A.

Câu 4: Công thức nghiệm tổng quát của phương trình \( - x + 2y = 0\) là

A. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = 2x\end{array} \right.\)

B. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = \frac{x}{2}\end{array} \right.\)

C. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y = \frac{{ - x}}{2}\end{array} \right.\)

D. \(\left\{ \begin{array}{l}x \in \mathbb{R}\\y =  - 2x\end{array} \right.\)

Phương pháp giải

Tìm \(y\) theo \(x\)

Lời giải

\( - x + 2y = 0 \Leftrightarrow \left\{ \begin{array}{l}x \in \mathbb{R}\\y = \frac{x}{2}\end{array} \right.\)

Đáp án B.

Câu 5: Rút gọn biểu thức \(2021\sqrt {{x^2}y}  + x\sqrt y \) với \(x < 0\) và \(y > 0\) ta được kết quả là:

A. \( - 2022x\sqrt y .\)

B. \( - 2020\sqrt {{x^2}y} .\)

C. \(2022x\sqrt y .\)

D. \( - 2020x\sqrt y .\)

Phương pháp giải

Sử dụng hằng đẳng thức: \(\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)

Lời giải

\(\begin{array}{l}\,\,\,\,2021\sqrt {{x^2}y}  + x\sqrt y \\ = 2021\left| x \right|\sqrt y  + x\sqrt y \\ =  - 2021x\sqrt y  + x\sqrt y \,\,\left( {do\,\,x < 0} \right)\\ = \left( { - 2021 + 1} \right)x\sqrt y \\ =  - 2020x\sqrt y \end{array}\)

Đáp án D.

Câu 6: Cho hai đường tròn \((O;5cm)\) và \((O';3cm)\). Nếu \(OO' = 2cm\) thì vị trí tương đối của hai đường tròn đó là

A. tiếp xúc trong.

B. tiếp xúc ngoài.

C. không giao nhau.

D. cắt nhau.

Phương pháp giải

Ta có: \(\left( {{O_1};{R_1}} \right);\left( {{O_2};{R_2}} \right)\)

So sánh \({R_1} + {R_2}\,,\,\left| {{R_1} - {R_2}} \right|\) với \({O_1}{O_2}\) và đưa ra nhận xét

Lời giải

Ta có: \(\left| {{R_{\left( O \right)}} - {R_{\left( {O'} \right)}}} \right| = \left| {5 - 3} \right| = 2cm = OO'\)

\( \Rightarrow \left( {O;5cm} \right)\) và \(\left( {O';3cm} \right)\) tiếp xúc trong.

Đáp án A.

Câu 7: Tính  \(\sqrt[3]{8} - \sqrt[3]{{ - 27}}\) ta được kết quả là

A. -19.

B. 5.

C. -1.

D. 1.

Phương pháp giải

\(\sqrt[3]{{{a^3}}} = a\) với mọi \(a\) xác định

Lời giải

\(\begin{array}{l}\,\,\,\,\sqrt[3]{8} - \sqrt[3]{{ - 27}}\\ = \sqrt[3]{{{2^3}}} - \sqrt[3]{{ - {3^3}}}\\ = 2 - \left( { - 3} \right)\\ = 2 + 3\\ = 5\end{array}\)

Đáp án A.

Câu 8: Các giá trị không âm của \(x\) để \(\sqrt x  < \sqrt 3 \) là

A. \(x > 3.\)

B. \(x = 3.\)

C. \(0 \le x < 3.\)

D. \(x < 3.\)

Phương pháp giải

Dựa vào điều kiện của đề bài, bình phương hai vế của bất phương trình

Lời giải

\(\sqrt x  < \sqrt 3  \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x < 3\end{array} \right. \Leftrightarrow 0 \le x < 3\)

Đáp án C.

Câu 9: Cho tam giác \(DEF\)vuông tại \(D\) có \(DE = 1cm,\,DF = \sqrt 3 cm\). Trong các khẳng định sau khẳng định nào đúng?

A. \(\sin F = \frac{1}{2}.\)

B. \(\tan F = \sqrt 3 .\)

C. \(\sin E = \frac{1}{2}.\)

D. \(\cos E = \frac{{\sqrt 3 }}{2}.\)

Phương pháp giải

Áp dụng định lý Py – ta – go, tính \(EF\)

Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông

Lời giải

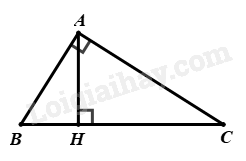
Tam giác \(DEF\) vuông tại \(D\), theo định lý Py – ta – go, ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,E{F^2} = D{F^2} + D{E^2}\\ \Leftrightarrow E{F^2} = {\left( {\sqrt 3 } \right)^2} + {1^2}\\ \Leftrightarrow E{F^2} = 4\\ \Rightarrow EF = 2\left( {cm} \right)\end{array}\)

Tam giác \(DEF\) vuông tại \(D\), áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông, ta có:

+ \(\sin F = \frac{{DE}}{{FE}} = \frac{1}{2}\)

Đáp án A.

Câu 10: Cho tam giác ABC vuông tại A, đường cao\(AH(H \in BC).\) Biết \(HB = 3cm;AH = 4cm.\) Độ dài \(HC\) là

A. \(\frac{{16}}{3}cm.\)

B. \(\frac{7}{3}cm.\)

C. \(3cm.\)

D. \(\frac{{25}}{3}cm.\)

Phương pháp giải

Áp dụng hệ thức lượng trong tam giác vuông

Lời giải

\(\Delta ABC\) vuông tại \(A\), đường cao \(AH\), ta có:

\(A{H^2} = BH.CH\) (hệ thức lượng trong tam giác vuông)

\( \Rightarrow CH = \frac{{A{H^2}}}{{BH}} = \frac{{{4^2}}}{3} = \frac{{16}}{3}\left( {cm} \right)\)

Đáp án A.

Câu 11: Cho \(a \le 5\), giá trị của biểu thức \(\sqrt {{a^2} - 10a + 25}  - 2a + 3\) bằng

A. \(8 + 3a.\)

B. \(3a - 8.\)

C. \(8 - 3a.\)

D. \(7 - 3a.\)

Phương pháp giải

Sử dụng hằng đẳng thức: \(\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)

Lời giải

\(\begin{array}{l}\,\,\,\,\sqrt {{a^2} - 10a + 25}  - 2a + 3\\ = \sqrt {{{\left( {a - 5} \right)}^2}}  - 2a + 3\\ = \left| {a - 5} \right| - 2a + 3\end{array}\)

\(\begin{array}{l} =  - \left( {a - 5} \right) - 2a + 3\,\,\,\left( {do\,\,a \le 5 \Rightarrow a - 5 \le 0 \Rightarrow \left| {a - 5} \right| =  - \left( {a - 5} \right)} \right)\\ =  - a + 5 - 2a + 3\\ =  - 3a + 8\end{array}\)

Đáp án C.

Câu 12: Cho tam giác ABC vuông tại A có BC = 2AB. Khi đó số đo góc B bằng

A. \({60^0}.\)

B. \({45^0}.\)

C. \({30^0}.\)

D. \({40^0}.\)

Phương pháp giải

Áp dụng tỉ số lượng giác của góc nhọn trong tam giác vuông

Lời giải

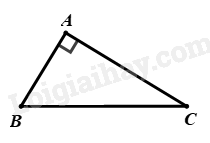
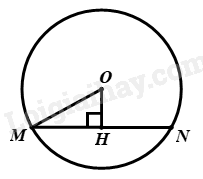
\(\Delta ABC\) vuông tại \(A\), ta có: \(\cos \angle B = \frac{{AB}}{{BC}}\) (tỉ số lượng giác của góc nhọn trong tam giác vuông)

\(\begin{array}{l} \Rightarrow \cos \angle B = \frac{{AB}}{{2AB}} = \frac{1}{2}\\ \Rightarrow \angle B = {60^0}\end{array}\)

Đáp án A.

Câu 13: Cho đường tròn \((O;6cm),\) có dây cung MN cách tâm O một khoảng bằng 3cm. Khi đó độ dài dây MN bằng

A. \(\sqrt 3 cm.\)

B. \(6\sqrt 3 cm.\)

C. \(3cm.\)

D. \(3\sqrt 3 cm.\)

Phương pháp giải

Kẻ \(OH \bot MN\)

Chứng minh \(H\) là trung điểm của \(MN\)

Áp dụng định lý Py – ta – go vào tam giác vuông \(OMH\), tính \(MH \Rightarrow MN\)

Lời giải

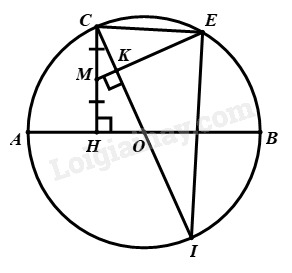
Xét \(\left( O \right)\): kẻ \(OH \bot MN\)

Vì khoảng cách từ tâm \(O\) đến dây cung \(MN\) bằng \(3cm \Rightarrow \)\(OH = 3\)

Ta có: \(OH \bot MN\) (cách dựng)

Mà \(OH\) là đường kính; \(MN\) là dây không đi qua tâm

\( \Rightarrow H\) là trung điểm của \(MN\)\( \Rightarrow HM = \frac{1}{2}MN\)

\(\Delta OHM\) vuông tại \(H\), theo định lý Py – ta – go, ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,O{M^2} = O{H^2} + M{H^2}\\ \Leftrightarrow {6^2} = {3^2} + M{H^2}\\ \Leftrightarrow M{H^2} = {6^2} - {3^2}\\ \Leftrightarrow M{H^2} = 27\\ \Rightarrow MH = 3\sqrt 3 \left( {cm} \right)\end{array}\)

\( \Rightarrow MN = 2MH = 2.3\sqrt 3  = 6\sqrt 3 \left( {cm} \right)\)

Đáp án B.

Câu 14: Tất cả các giá trị của \(x\) để biểu thức \(\sqrt {1 - x} \) có nghĩa là

A. \(x \ge 0\).

B. \(x > 1\).

C. \(x \ge  - 1\).

D. \(x \le 1\).

Phương pháp giải

Biểu thức \(\sqrt {f\left( x \right)} \) có nghĩa \( \Leftrightarrow f\left( x \right) \ge 0\)

Lời giải

Biểu thức \(\sqrt {1 - x} \) có nghĩa \( \Leftrightarrow 1 - x \ge 0 \Leftrightarrow x \le 1\)

Đáp án D.

Câu 15: Hàm số \(y = ({m^2} - 1)x + m\)(\(m\) là tham số) là hàm số bậc nhất khi

A. \(m \ne  \pm 1{\rm{ }}{\rm{.}}\)

B. \(m \ne 0.\)

C. \(m = 1.\)

D. \(m \ne 1.\)

Phương pháp giải

Hàm số \(y = ax + b\) là hàm số bậc nhất \( \Leftrightarrow a \ne 0\)

Lời giải

Hàm số \(y = \left( {{m^2} - 1} \right)x + m\) là hàm số bậc nhất \( \Leftrightarrow {m^2} - 1 \ne 0 \Leftrightarrow m \ne  \pm 1\)

Đáp án A.

Phần tự luận

Bài 1: (3,0 điểm)

1) Tính giá trị của biểu thức \(\sqrt {{{\left( {\sqrt 2  - 1} \right)}^2}}  - \sqrt 2 .\)

2) Hàm số \(y = \left( {2 - \sqrt 5 } \right)x - 2\)đồng biến hay nghịch biến trên \(\mathbb{R}\)? Vì sao?

3) Tìm các giá trị của tham số \(m\)để đường thẳng \((d):y = (m - 3)x + 2\) đi qua điểm \(A\left( { - 1;5} \right)\).

Phương pháp giải

1) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\)

2) Hàm số \(y = ax + b\) đồng biến trên \(\mathbb{R}\) nếu \(a > 0\), nghịch biến trên \(\mathbb{R}\) nếu \(a < 0\)

3) Điểm \(M\left( {{x_0};{y_0}} \right)\) thuộc đồ thị hàm số \(y = ax + b\) nếu \({y_0} = a{x_0} + b\)

Lời giải

1) \(\sqrt {{{\left( {\sqrt 2  - 1} \right)}^2}}  - \sqrt 2 \)

\(\begin{array}{l} = \left| {\sqrt 2  - 1} \right| - \sqrt 2 \\ = \sqrt 2  - 1 - \sqrt 2 \,\,\,\left( {do\,\,\sqrt 2  > 1 \Rightarrow \sqrt 2  - 1 > 0} \right)\\ =  - 1\end{array}\)

2) Vì \(2 - \sqrt 5  < 0\) nên hàm số \(y = \left( {2 - \sqrt 5 } \right)x - 2\) nghịch biến trên \(\mathbb{R}\).

3) Vì \(\left( d \right):y = \left( {m - 3} \right)x + 2\) đi qua điểm \(A\left( { - 1;5} \right)\) nên ta có:

\(\begin{array}{l}\,\,\,\,\,\,\,\left( {m - 3} \right).\left( { - 1} \right) + 2 = 5\\ \Leftrightarrow  - m + 3 + 2 = 5\\ \Leftrightarrow  - m = 0\\ \Leftrightarrow m = 0\end{array}\)

Vậy \(m = 0\)

Bài 2: (1,5 điểm)

Cho biểu thức \(A = \frac{{x + 1}}{{x - 1}} - \frac{1}{{\sqrt x  + 1}} - \frac{1}{{\sqrt x  - 1}}\) với \(x \ge 0\), \(x \ne 1\).

1) Rút gọn biểu thức \(A.\)

2) Tính giá trị của biểu thức \(A\)  tại \(x = 4 + 2\sqrt 3 .\)

Phương pháp giải

a) Vận dụng hằng đẳng thức \(a - b = \left( {\sqrt a  - \sqrt b } \right)\left( {\sqrt a  + \sqrt b } \right)\) xác định mẫu thức chung của biểu thức

Quy đồng các phân thức, thực hiện các phép toán từ đó rút gọn được biểu thức.

b) Sử dụng hằng đẳng thức: \(\sqrt {{A^2}}  = \left| A \right| = \left\{ \begin{array}{l}A\,\,\,khi\,\,A \ge 0\\ - A\,\,\,khi\,\,A < 0\end{array} \right.\), tính \(\sqrt x \)

Thay vào biểu thức \(A\), tính

Lời giải

a) \(A = \frac{{x + 1}}{{x - 1}} - \frac{1}{{\sqrt x  + 1}} - \frac{1}{{\sqrt x  - 1}}\)

\(\begin{array}{l}A = \frac{{x + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} - \frac{1}{{\sqrt x  + 1}} - \frac{1}{{\sqrt x  - 1}}\\A = \frac{{x + 1 - \left( {\sqrt x  - 1} \right) - \left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\A = \frac{{x + 1 - \sqrt x  + 1 - \sqrt x  - 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\A = \frac{{x - 2\sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\A = \frac{{{{\left( {\sqrt x  - 1} \right)}^2}}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\A = \frac{{\sqrt x  - 1}}{{\sqrt x  + 1}}\end{array}\)

Vậy \(A = \frac{{\sqrt x  - 1}}{{\sqrt x  + 1}}\) với \(x \ge 0;x \ne 1\)

b) Ta có: \(x = 4 + 2\sqrt 3  = 3 + 2\sqrt 3  + 1 = \left( {\sqrt 3  + 1} \right)\)

\( \Rightarrow \sqrt x  = \sqrt {{{\left( {\sqrt 3  + 1} \right)}^2}}  = \left| {\sqrt 3  + 1} \right| = \sqrt 3  + 1\,\,\,\left( {do\,\,\sqrt 3  + 1 > 0} \right)\)

Thay vào \(A\), ta được: \(A = \frac{{\sqrt 3  + 1 - 1}}{{\sqrt 3  + 1 + 1}} = \frac{{\sqrt 3 }}{{\sqrt 3  + 2}}\)

Đáp án A.

Bài 3: (2,0 điểm)

Cho đường tròn (O) đường kính AB, C là điểm bất kỳ trên đường tròn (C khác A, B). Gọi H là hình chiếu của C trên AB, M là trung điểm của CH. Kẻ tia MK vuông góc với CO (K thuộc OC) cắt đường tròn (O) tại E. Kẻ đường kính CI của đường tròn (O) . Chứng minh:

1) \(CE \bot EI.\)

2) Tam giác \(CEH\)cân.

Phương pháp giải

a) Góc nội tiếp chắn nửa đường tròn bằng \({90^0} \Rightarrow CE \bot EI\)

b) \(\frac{{C{H^2}}}{2} = \frac{{C{E^2}}}{2} = CK.CO \Rightarrow CH = CE \Rightarrow \Delta CHE\) cân

Lời giải

a) \(CI\) là đường kính của đường tròn \(\left( O \right)\), mà \(E \in \left( O \right)\)

\( \Rightarrow \angle CEI = {90^0}\) (góc nội tiếp chắn nửa đường tròn)

\( \Rightarrow CE \bot EI\)

b) Xét \(\Delta CKM\) và \(\Delta CHO\) có:

$\left. \begin{align} \angle HCO\,\,chung \\  \angle CKM=\angle CHO={{90}^{0}} \\ \end{align} \right\}\Rightarrow \Delta CKM\backsim \Delta CHO\left( g.g \right)$

\(\begin{array}{l} \Rightarrow \frac{{CK}}{{CM}} = \frac{{HC}}{{CO}}\\ \Leftrightarrow CK.CO = CM.HC\\ \Leftrightarrow CK.CO = CM.2CM\\ \Leftrightarrow 2C{M^2} = CK.CO\end{array}\)

Có \(\frac{{C{H^2}}}{2} = \frac{{{{\left( {2CM} \right)}^2}}}{2} = 2C{M^2}\)

\( \Rightarrow \frac{{C{H^2}}}{2} = CK.CO\,\,\,\,\left( 1 \right)\)

Xét \(\Delta CEI\) có: \(EK \bot CI,\angle CEI = {90^0}\)

\(\begin{array}{l} \Rightarrow C{E^2} = CK.CI = 2CK.2CO\\ \Leftrightarrow \frac{{C{E^2}}}{2} = CK.CO\,\,\,\,\,\left( 2 \right)\end{array}\)

Từ (1) và (2), suy ra \(\frac{{C{H^2}}}{2} = \frac{{C{E^2}}}{2} = CK.CO\)

\( \Rightarrow CH = CE\)

\( \Rightarrow \Delta CHE\) cân tại \(C\)

Bài 4: (0,5 điểm) Cho  các số thực \(x,\,y\)thỏa mãn \(\left( {x + \sqrt {2021 + {x^2}} } \right)\left( {y + \sqrt {2021 + {y^2}} } \right) = 2021\). Tính giá trị của biểu thức: \(M = {x^{2021}} + {y^{2021}} + 2022\).

Phương pháp giải

Thực hiện nhân liên hợp (*) với \(x - \sqrt {2021 + {x^2}} \), ta được phương trình (1)

Thực hiện nhân liên hợp (*) với \(y - \sqrt {2021 + {y^2}} \), ta được phương trình (2)

Cộng (1) và (2), ta tìm được \(x\) theo \(y\)

Thay vào \(M\) và tính.

Lời giải

\(\left( {x + \sqrt {2021 + {x^2}} } \right)\left( {y + \sqrt {2021 + {y^2}} } \right) = 2021\)   (*)

Thực hiện nhân liên hợp (*) với \(x - \sqrt {2021 + {x^2}} \), ta được:

\(\begin{array}{l}\,\,\,\,\,\,\,\,\left( {x + \sqrt {2021 + {x^2}} } \right)\left( {x - \sqrt {2021 + {x^2}} } \right)\left( {y + \sqrt {2021 + {y^2}} } \right) = 2021\left( {x - \sqrt {2021 + {x^2}} } \right)\\ \Leftrightarrow \left( {{x^2} - 2021 - {x^2}} \right)\left( {y + \sqrt {2021 + {y^2}} } \right) = 2021\left( {x - \sqrt {2021 + {x^2}} } \right)\\ \Leftrightarrow  - 2021\left( {y + \sqrt {2021 + {y^2}} } \right) = 2021\left( {x - \sqrt {2021 + {x^2}} } \right)\\ \Leftrightarrow  - y - \sqrt {2021 + {y^2}}  = x - \sqrt {2021 + {x^2}} \,\,\,\,\,\,\left( 1 \right)\end{array}\)

Thực hiện nhân liên hợp (*) với \(y - \sqrt {2021 + {y^2}} \), ta được:

\(\begin{array}{l}\,\,\,\,\,\,\,\,\left( {x + \sqrt {2021 + {x^2}} } \right)\left( {y + \sqrt {2021 + {y^2}} } \right)\left( {y - \sqrt {2021 + {y^2}} } \right) = 2021\left( {y - \sqrt {2021 + {y^2}} } \right)\\ \Leftrightarrow \left( {x + \sqrt {2021 + {x^2}} } \right)\left( {{y^2} - 2021 - {y^2}} \right) = 2021\left( {y - \sqrt {2021 + {y^2}} } \right)\\ \Leftrightarrow  - 2021\left( {x + \sqrt {2021 + {x^2}} } \right) = 2021\left( {y - \sqrt {2021 + {y^2}} } \right)\\ \Leftrightarrow  - x - \sqrt {2021 + {x^2}}  = y - \sqrt {2021 + {y^2}} \,\,\,\,\,\,\left( 2 \right)\end{array}\)

Cộng (1) và (2), ta được:

\(\begin{array}{l}\,\,\,\,\,\,\,\, - y - x = x + y\\ \Leftrightarrow  - 2y = 2x\\ \Leftrightarrow x =  - y\end{array}\)

\(\begin{array}{l}M = {x^{2021}} + {y^{2021}} + 2022\\M = {\left( { - y} \right)^{2021}} + {y^{2021}} + 2022\\M =  - {y^{2021}} + {y^{2021}} + 2022\\M = 2022\end{array}\)