Đề kiểm tra giữa kì 1 Toán 9 - Đề số 6 có lời giải chi tiếtTải về Đề kiểm tra giữa kì 1 Toán 9 - Đề số 6 có lời giải chi tiết Quảng cáo
Đề bài Phần trắc nghiệm (1 điểm) Câu 1. Căn bậc hai của 9 là:
Câu 2. \(\sqrt {3 - 5x} \) xác định khi và chỉ khi
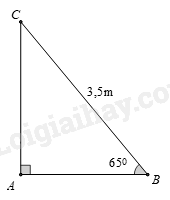
Câu 3. Một cái thang dài \(3,5\,{\rm{m}}\) đặt dựa vào tường, góc “an toàn” giữa thang và mặt đất để thang không đổ khi người trèo lên là \(65^\circ \) . Khoảng cách “an toàn” từ chân tường đến chân thang (Kết quả làm tròn đến chữ số thập phân thứ nhất) là:
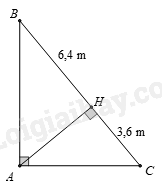
Câu 4. Tam giác \(ABC\) vuông tại \(A\) , có đường cao \(AH\) chia cạnh huyền thành hai đoạn thẳng có độ dài \(3,6\,{\rm{cm}}\) và \(6,4\,{\rm{cm}}\) . Độ dài một trong các cạnh góc vuông là
Phần tự luận (9 điểm) Bài 1 (1,5 điểm) Thực hiện phép tính. a) \(\sqrt {20} + 2\sqrt {45} - 15\sqrt {\frac{1}{5}} \) . b)\(\frac{{\sqrt {35} - \sqrt 7 }}{{\sqrt 5 - 1}} + \frac{{12}}{{\sqrt 7 - 1}}\) . c)\(\sqrt {8 + 2\sqrt 7 } - \sqrt {28} \) . Bài 2 (2 điểm) Giải các phương trình sau: a) \(\sqrt {7x - 3} = 5\) .
b) \(5\sqrt {4x - 16} - \frac{7}{3}\sqrt {9x - 36} = 36 - 3\sqrt {x - 4} \) .
c) \(\sqrt {{x^2} - 36} - \sqrt {x - 6} = 0\) .
d) \({x^2} + 2 = \sqrt {3 - 4x + 2{x^2} + 4{x^3}} \) .
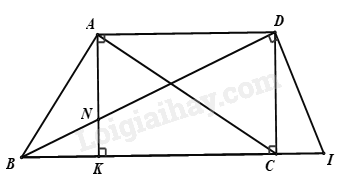
Bài 3 (2 điểm) Cho biểu thức \(M = \frac{{\sqrt x - 1}}{{\sqrt x }}\) và \(P = \frac{{\sqrt x - 2}}{{\sqrt x + 1}} + \frac{{2 + 8\sqrt x }}{{x - 1}} - \frac{2}{{1 - \sqrt x }}\) với \(x > 0;\,\,x \ne 1;x \ne 5\) a) Tính giá trị của \(M\) khi \(x = 9\) . b) Chứng minh \(P = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\) . c) Đặt \(Q = M.P + \frac{{x - 5}}{{\sqrt x }}\) . Hãy so sánh \(Q\) với 3. Bài 4 (3,5 điểm): Cho tam giác \(ABC\) nhọn , đường cao \(AK\) . a) Giải tam giác \(ACK\) biết \(\widehat C = 30^\circ ,\,AK = 3\,{\rm{cm}}\) . b) Chứng minh \(AK = \frac{{BC}}{{\cot B + \cot C}}\) . c) Biết \(BC = 5\,{\rm{cm}},\widehat B = 68^\circ ,\widehat C = 30^\circ \) . Tính diện tích tam giác \(ABC\) ( kết quả làm tròn chữ số thập phân thứ nhất). d) Vẽ hình chữ nhật \(CKAD\) , \(DB\) cắt \(AK\) tại \(N\) . Chứng minh rằng \(\frac{1}{{A{K^2}}} = \frac{{{{\cot }^2}\widehat {ACB}}}{{D{N^2}}} + \frac{1}{{D{B^2}}}\) . -------- Hết -------- Lời giải chi tiết HƯỚNG DẪN GIẢI CHI TIẾT THỰC HIỆN: BAN CHUYÊN MÔN LOIGIAIHAY.COM Phần trắc nghiệm
Câu 1. Căn bậc hai của 9 là:
Phương pháp Dựa vào kiến thức về căn bậc 2. Lời giải Căn bậc hai của số \(9\) là \( \pm 3\) . Đáp án B. Câu 2. \(\sqrt {3 - 5x} \) xác định khi và chỉ khi
Phương pháp Biểu thức chứa căn bậc hai xác định khi biểu thức trong căn lớn hơn hoặc bằng 0. Lời giải Biểu thức xác định khi \(3 - 5x \ge 0 \Leftrightarrow x \le \frac{3}{5}\) . Đáp án C. Câu 3. Một cái thang dài \(3,5\,{\rm{m}}\) đặt dựa vào tường, góc “an toàn” giữa thang và mặt đất để thang không đổ khi người trèo lên là \(65^\circ \) . Khoảng cách “an toàn” từ chân tường đến chân thang (Kết quả làm tròn đến chữ số thập phân thứ nhất) là:
Phương pháp Sử dụng tỉ số lượng giác của góc nhọn. Lời giải Chiều dài thang là \(BC = 3,5\,{\rm{m}}\) . Góc “an toàn” là \(\widehat {ABC} = 56^\circ \) . Khoảng cách an toàn là \(AB\) . Áp dụng tỉ số lượng giác của góc nhọn cho tam giác vuông \(ABC\) ta có: \(\cos B = \frac{{AB}}{{BC}} \Rightarrow AB = BC.\cos B = 3,5.\cos 65^\circ \approx 1,5\,{\rm{m}}\) . Đáp án D. Câu 4. Tam giác \(ABC\) vuông tại \(A\) , có đường cao \(AH\) chia cạnh huyền thành hai đoạn thẳng có độ dài \(3,6\,{\rm{cm}}\) và \(6,4\,{\rm{cm}}\) . Độ dài một trong các cạnh góc vuông là
Phương pháp Dựa vào hệ thức lượng trong tam giác vuông. Lời giải Giả sử \(HC = 3,6\,{\rm{cm}}\) và \(HB = 6,4\,{\rm{cm}} \Rightarrow BC = HC + HB = 10\,{\rm{cm}}\) . Áp dụng hệ thức lượng cho tam giác vuông \(ABC\) ta có: \(A{B^2} = BH.BC = 6,4.10 = 64 \Rightarrow AB = 8\,{\rm{cm}}\) Đáp án A. Phần tự luận. Bài 1 (1,5 điểm) Thực hiện phép tính. a) \(\sqrt {20} + 2\sqrt {45} - 15\sqrt {\frac{1}{5}} \) . b)\(\frac{{\sqrt {35} - \sqrt 7 }}{{\sqrt 5 - 1}} + \frac{{12}}{{\sqrt 7 - 1}}\) . c)\(\sqrt {8 + 2\sqrt 7 } - \sqrt {28} \) . Phương pháp Sử dụng quy tắc tính với căn bậc hai. Lời giải a)\(\sqrt {20} + 2\sqrt {45} - 15\sqrt {\frac{1}{5}} \) \( = \sqrt {4.5} + 2\sqrt {9.5} - 15\frac{{\sqrt 5 }}{5}\) \( = 2.\sqrt 5 + 2.3\sqrt 5 - 3\sqrt 5 \) \( = 5\sqrt 5 \) . b).\(\frac{{\sqrt {35} - \sqrt 7 }}{{\sqrt 5 - 1}} + \frac{{12}}{{\sqrt 7 - 1}}\) \( = \frac{{\sqrt 7 .\sqrt 5 - \sqrt 7 }}{{\sqrt 5 - 1}} + \frac{{12}}{{\sqrt 7 - 1}}\) \( = \frac{{\sqrt 7 .(\sqrt 5 - 1)}}{{\sqrt 5 - 1}} + \frac{{12(\sqrt 7 + 1)}}{{(\sqrt 7 )_{}^2 - 1}}\) \( = \sqrt 7 + \frac{{12(\sqrt 7 + 1)}}{6}\) \( = \sqrt 7 + 2(\sqrt 7 + 1)\) \( = 3\sqrt 7 + 2\) . c).\(\sqrt {8 + 2\sqrt 7 } - \sqrt {28} \) \( = \sqrt {(1 + \sqrt 7 } )_{}^2 - \sqrt {4.7} \) \( = \left| {1 + \sqrt 7 } \right| - 2\sqrt 7 \) \( = 1 + \sqrt 7 - 2\sqrt 7 \) \( = 1 - \sqrt 7 \) . Bài 2 (2 điểm) Giải các phương trình sau: a) \(\sqrt {7x - 3} = 5\) .
b) \(5\sqrt {4x - 16} - \frac{7}{3}\sqrt {9x - 36} = 36 - 3\sqrt {x - 4} \) .
c) \(\sqrt {{x^2} - 36} - \sqrt {x - 6} = 0\) .
d) \({x^2} + 2 = \sqrt {3 - 4x + 2{x^2} + 4{x^3}} \) .
Phương pháp Xác định điều kiện xác định của phương trình. a) Bình phương hai vế để tìm x. b) Rút nhân tử chung ra ngoài để nhóm nhân tử chung. c) Sử dụng hằng đẳng thức để nhóm nhân tử chung. d) Bình phương hai vế để tìm x. Lời giải a) Điều kiện: \(x \ge \frac{3}{7}\) . Bình phương hai vế của phương trình ta được: \(7x - 3 = 25 \Leftrightarrow x = 4\) ( thỏa mãn điều kiện) . Vậy tập nghiệm của phương trình là: \(S = \left\{ 4 \right\}\) . b) Điều kiện: \(x \ge 4\) . \(5\sqrt {4x - 16} - \frac{7}{3}\sqrt {9x - 36} = 36 - 3\sqrt {x - 4} \) \( \Leftrightarrow 5\sqrt {4\left( {x - 4} \right)} - \frac{7}{3}\sqrt {9\left( {x - 4} \right)} = 36 - 3\sqrt {x - 4} \Leftrightarrow 10\sqrt {x - 4} - \frac{7}{3}.3\sqrt {x - 4} = 36 - 3\sqrt {x - 4} \) \( \Leftrightarrow 6\sqrt {x - 4} = 36 \Leftrightarrow \sqrt {x - 4} = 6 \Leftrightarrow x - 4 = 36 \Leftrightarrow x = 40\) ( thỏa mãn điều kiện) . Vậy tập nghiệm của phương trình là: \(S = \left\{ {40} \right\}\) . c) Điều kiện: \(x \ge 6\) . \(\sqrt {{x^2} - 36} - \sqrt {x - 6} = 0 \Leftrightarrow \sqrt {x - 6} .\sqrt {x + 6} - \sqrt {x - 6} = 0\) \( \Leftrightarrow \sqrt {x - 6} \left( {\sqrt {x + 6} - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}\sqrt {x - 6} = 0\\\sqrt {x + 6} = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 6\left( {tm} \right)\\x = - 5\left( L \right)\end{array} \right.\) . Vậy tập nghiệm của phương trình là: \(S = \left\{ 6 \right\}\) . d) Điều kiện: \(3 - 4x + 2{x^2} + 4{x^3} \ge 0\) . Bình phương hai vế của phương trình ta được: \({x^4} + 4{x^2} + 4 = 3 - 4x + 2{x^2} + 4{x^3} \Leftrightarrow {x^4} - 4{x^3} + 2{x^2} + 4x + 1 = 0\,\,\,\left( 1 \right)\) Nhận xét: \(x = 0\) không phải là nghiệm của phương trình \(\left( 1 \right)\) , chia cả hai vế của phương trình \(\left( 1 \right)\) cho \({x^2}\) ta được: \({x^2} - 4x + 2 + \frac{4}{x} + \frac{1}{{{x^2}}} = 0 \Leftrightarrow {x^2} + \frac{1}{{{x^2}}} - 4\left( {x - \frac{1}{x}} \right) + 2 = 0\,\,\,\left( 2 \right)\) . Đặt \(x - \frac{1}{x} = a \Rightarrow {a^2} = {x^2} + \frac{1}{{{x^2}}} - 2 \Leftrightarrow {x^2} + \frac{1}{{{x^2}}} = {a^2} + 2\) . Phương trình \(\left( 2 \right)\) trở thành: \({a^2} + 2 - 4a + 2 = 0 \Leftrightarrow {\left( {a - 2} \right)^2} = 0 \Leftrightarrow a = 2\) . Với \(a = 2 \Rightarrow x - \frac{1}{x} = 2 \Leftrightarrow {x^2} - 2x - 1 = 0 \Leftrightarrow {\left( {x - 1} \right)^2} = \sqrt 2 \Leftrightarrow x = 1 \pm \sqrt 2 \) ( thỏa mãn điều kiện) Vậy tập nghiệm của phương trình là: \(S = \left\{ {1 - \sqrt 2 ;\,\,1 + \sqrt 2 } \right\}\) . Bài 3 (2 điểm) Cho biểu thức \(M = \frac{{\sqrt x - 1}}{{\sqrt x }}\) và \(P = \frac{{\sqrt x - 2}}{{\sqrt x + 1}} + \frac{{2 + 8\sqrt x }}{{x - 1}} - \frac{2}{{1 - \sqrt x }}\) với \(x > 0;\,\,x \ne 1;x \ne 5\) a) Tính giá trị của \(M\) khi \(x = 9\) . b) Chứng minh \(P = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\) . c) Đặt \(Q = M.P + \frac{{x - 5}}{{\sqrt x }}\) . Hãy so sánh \(Q\) với 3. Phương pháp a) Kiểm tra x = 9 có thỏa mãn điều kiện hay không, sau đó thay vào biểu thức A để tính. b) Xác định mẫu thức chung, quy đồng và thực hiện các phép toán với các phân thức đại số. c) Thay M và Q bằng biểu thức rút gọn để có Q. Tính Q – 3, so sánh với 0. Lời giải a) Thay \(x = 9\) ( thỏa mãn điều kiện) vào \(M\) ta được: \(M = \frac{{\sqrt 9 - 1}}{{\sqrt 9 }} = \frac{{3 - 1}}{3} = \frac{2}{3}\) . Vậy \(x = 9\) thì \(M = \frac{2}{3}\) . b) Ta có: \(P = \frac{{\sqrt x - 2}}{{\sqrt x + 1}} + \frac{{2 + 8\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} + \frac{2}{{\sqrt x - 1}} = \frac{{\left( {\sqrt x - 2} \right)\left( {\sqrt x - 1} \right) + 2 + 8\sqrt x + 2\left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\) \( = \frac{{x - 3\sqrt x + 2 + 2 + 8\sqrt x + 2\sqrt x + 2}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{x + 7\sqrt x + 6}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{\left( {\sqrt x + 1} \right)\left( {\sqrt x + 6} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\) ( điều phải chứng minh) . Vậy \(P = \frac{{\sqrt x + 6}}{{\sqrt x - 1}}\) . c) Ta có: \(Q = M.P + \frac{{x - 5}}{{\sqrt x }} = \frac{{\sqrt x - 1}}{{\sqrt x }}.\frac{{\sqrt x + 6}}{{\sqrt x - 1}} + \frac{{x - 5}}{{\sqrt x }} = \frac{{\sqrt x + 6}}{{\sqrt x }} + \frac{{x - 5}}{{\sqrt x }} = \frac{{x + \sqrt x + 1}}{{\sqrt x }}\) . Xét \(Q - 3 = \frac{{x + \sqrt x + 1}}{{\sqrt x }} - 3 = \frac{{x - 2\sqrt x + 1}}{{\sqrt x }} = \frac{{{{\left( {\sqrt x - 1} \right)}^2}}}{{\sqrt x }} > 0\) với mọi \(x > 0;\,\,x \ne 1\) . Do đó \(Q > 3\) . Bài 4 (3,5 điểm): Cho tam giác \(ABC\) nhọn , đường cao \(AK\) . a) Giải tam giác \(ACK\) biết \(\widehat C = 30^\circ ,\,AK = 3\,{\rm{cm}}\) . b) Chứng minh \(AK = \frac{{BC}}{{\cot B + \cot C}}\) . c) Biết \(BC = 5\,{\rm{cm}},\widehat B = 68^\circ ,\widehat C = 30^\circ \) . Tính diện tích tam giác \(ABC\) ( kết quả làm tròn chữ số thập phân thứ nhất). d) Vẽ hình chữ nhật \(CKAD\) , \(DB\) cắt \(AK\) tại \(N\) . Chứng minh rằng \(\frac{1}{{A{K^2}}} = \frac{{{{\cot }^2}\widehat {ACB}}}{{D{N^2}}} + \frac{1}{{D{B^2}}}\) . Phương pháp a) Sử dụng các kiến thức về tam giác để giải tam giác. b) Biểu diễn tỉ số lượng giác cotB và cotC theo AK và BC để chứng minh. c) \({S_{\Delta ABC}} = \frac{1}{2}AK.BC\) . Sử dụng các tỉ số lượng giác để tính AK. d) ) Kẻ \(DI \bot BD\) tại \(D\) . Chứng minh suy ra tỉ lệ của các cạnh tương ứng để chứng minh điều phải chứng minh. Lời giải a) Xét tam giác \(ACK\) vuông tại \(K\) có \(\widehat C = 30^\circ \Rightarrow \widehat B = 60^\circ \) ( theo định lí tổng ba góc trong tam giác). \(\sin \widehat C = \frac{{AK}}{{AC}} \Rightarrow \sin 30^\circ = \frac{3}{{AC}} \Rightarrow \frac{1}{2} = \frac{3}{{AC}} \Rightarrow AC = 6\) (cm) Theo định lí Pitago trong tam giác vuông \(ACK\) ta có \(KC = \sqrt {A{C^2} - A{K^2}} = \sqrt {{6^2} - {3^2}} = \sqrt {27} = 3\sqrt 3 \) (cm). b) Xét tam giác vuông \(AKB\) ta có \(\cot B = \frac{{BK}}{{AK}}\) Xét tam giác vuông \(AKC\) ta có \(\cot C = \frac{{KC}}{{AK}}\) Nên \(\cot B + \cot C = \frac{{BK}}{{AK}} + \frac{{KC}}{{AK}} = \frac{{BK + KC}}{{AK}} = \frac{{BC}}{{AK}}\) Vậy \(AK = \frac{{BC}}{{\cot B + \cot C}}\) (đpcm). c) Xét tam giác vuông \(AKB\) ta có \(\tan B = \frac{{AK}}{{BK}} \Rightarrow AK = \tan B.BK\) Xét tam giác vuông \(AKC\) ta có \(\tan C = \frac{{AK}}{{CK}} \Rightarrow AK = \tan C.CK\) Từ đó ta có \(\tan B.BK = \tan C.KC \Rightarrow \frac{{\tan B}}{{\tan C}} = \frac{{KC}}{{BK}} \Rightarrow \frac{{\tan 68^\circ }}{{\tan 30^\circ }} = \frac{{KC}}{{BK}} \Rightarrow \frac{{KC}}{{BK}} \approx 4,3 = \frac{{43}}{{10}}\) . Mà \(KC = BC - BK = 5 - BK \Rightarrow \frac{{5 - BK}}{{BK}} = \frac{{43}}{{10}} \Rightarrow \frac{5}{{BK}} = \frac{{53}}{{10}}\) . Vậy \(BK = 0,9;\;KC = 4,1\) . Xét tam giác vuông \(AKC\) có \(\tan C = \frac{{AK}}{{CK}} \Rightarrow \tan 30^\circ = \frac{{AK}}{{CK}} \Rightarrow \frac{{\sqrt 3 }}{3} = \frac{{AK}}{{CK}} \Rightarrow AK = \frac{{\sqrt 3 }}{3}.CK = 2,4\) (cm). Vậy \({S_{\Delta ABC}} = \frac{1}{2}AK.BC = \frac{1}{2}.2,4.5 = 6\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\) . d) Kẻ \(DI \bot BD\) tại \(D\) khi đó \(\widehat {ADN} = \widehat {CDI}\) ( cùng phụ với \(\widehat {CDN}\) ), Khi đó Suy ra \(\frac{{AD}}{{CD}} = \frac{{AN}}{{CI}} = \frac{{DN}}{{DI}} \Rightarrow AD.DI = DN.DC \Rightarrow \frac{{DN}}{{DI}} = \frac{{AD}}{{DC}} \Rightarrow \frac{{N{D^2}}}{{D{I^2}}} = \frac{{A{D^2}}}{{D{C^2}}}\) Vì \(AK = DC\) ( tính chất hcn) \(\widehat {ACB} = \widehat {DAC} \Rightarrow {\cot ^2}\widehat {ACB} = {\cot ^2}\widehat {DAC} = \frac{{A{D^2}}}{{D{C^2}}} = \frac{{N{D^2}}}{{D{I^2}}}\) Điều cần chứng minh tương đương với \(\frac{1}{{D{C^2}}} = \frac{{N{D^2}}}{{D{I^2}.D{N^2}}} + \frac{1}{{D{B^2}}} \Leftrightarrow \frac{1}{{D{C^2}}} = \frac{1}{{D{I^2}.}} + \frac{1}{{D{B^2}}}\) (luôn đúng theo hệ thức lượng trong tam giác vuông \(BDI\) có đường cao \(DC\) ). (đpcm).
|




















Danh sách bình luận