Đề thi học kì 2 môn toán lớp 9 năm 2019 - 2020 PGD quận Hà Đông

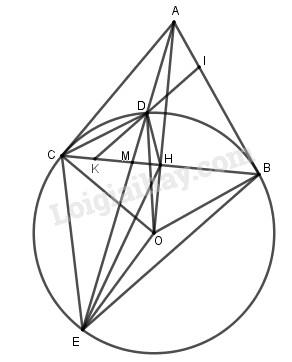
Đề bài

Bài 1  (2,0 điểm):

Cho các biểu thức \(A = \dfrac{{\sqrt x  - 1}}{{\sqrt x  - 3}}\)  và \(B = \dfrac{{\sqrt x  + 3}}{{\sqrt x  + 1}} - \dfrac{5}{{1 - \sqrt x }} + \dfrac{4}{{x - 1}}\) với \(x \ge 0;x \ne 1;x \ne 9\)

1) Tính giá trị của A khi \(x = 36.\)

2) Rút gọn biểu thức B

3) Đặt \(P = A.B.\) Tìm \(x \in \mathbb{N}\) để P có giá trị lớn nhất

Bài 2 (2,5 điểm):

1) Khi uống trà sữa, người ta thường dùng ống hút bằng nhựa hình trụ có đường kính đáy 0,9cm, độ dài trục 21cm. Hỏi khi thải ra ngoài môi trường, diện tích nhựa gây ô nhiễm môi trường do 1000 ống hút gây ra là bao nhiêu?

2) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

Một người mua một cái bàn là và một cái quạt điện với tổng số tiền theo giá niêm yết là 850 nghìn đồng. Khi trả tiền người đó được khuyến mại giảm 20% đối với giá tiền bàn là và 10% đối với giá tiền quạt điện so với giá niêm yết. Vì vậy, người đó phải trả tổng cộng 740 nghìn đồng. Tính giá tiền của cái bàn là và cái quạt điện theo giá niêm yết.

Bài 3 (2,0 điểm):

1) Giải hệ phương trình \(\left\{ \begin{array}{l}2\sqrt {x - 2}  + \sqrt {y - 1}  = 5\\\sqrt {x - 2}  + \sqrt {y - 1}  = 3\end{array} \right.\)

2) Cho phương trình \({x^4} - 2m{x^2} + {m^2} - 4 = 0\)

a) Giải phương trình với \(m = 3.\)

b) Tìm m để phương trình có 3 nghiệm phân biệt

Bài 4 (3,0 điểm):

Từ điểm A ở ngoài đường tròn \(\left( {O;R} \right)\) vẽ hai tiếp tuyến AB, AC (B, C là các tiếp điểm) và cát tuyến ADE thuộc nửa mặt phẳng bờ là đường thẳng OA không chứa điểm B của đường tròn (O). Gọi H là giao điểm của OA và BC.

1) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn

2) Chứng minh \(AO \bot BC\) tại H và \(AH.AO = AD.AE\)

3) Đường thẳng đi qua điểm D và song song với đường thẳng BE cắt AB, BC lần lượt tại I, K. Chứng minh tứ giác OHDE nội tiếp và D là trung điểm của IK.

Bài 5 (0,5 điểm):

Cho ba số thực \(x,y,z > 0\) thỏa mãn \(x + y + z \ge 6.\)

Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^3} + {y^3}}}{{{x^2} + {y^2}}} + \dfrac{{{y^3} + {z^3}}}{{{y^2} + {z^2}}}\) \( + \dfrac{{{z^3} + {x^3}}}{{{z^2} + {x^2}}}\)

HẾT

LG bài 1

Phương pháp giải:

1) Thay \(x = 36\) vào biểu thức A rồi tính toán

2) Quy đồng mẫu, cộng trừ các phân thức để rút gọn B

3) Đánh giá \(P \le a\) để xác định được giá trị lớn nhất của P là \(a\), từ đó ta tìm được \(x.\)

Lời giải chi tiết:

Cho các biểu thức \(A = \dfrac{{\sqrt x  - 1}}{{\sqrt x  - 3}}\)  và \(B = \dfrac{{\sqrt x  + 3}}{{\sqrt x  + 1}} - \dfrac{5}{{1 - \sqrt x }} + \dfrac{4}{{x - 1}}\) với \(x \ge 0;x \ne 1;x \ne 9\)

1) Tính giá trị của A khi \(x = 36.\)

Thay \(x = 36\) (thỏa mãn điều kiện) vào biểu thức A ta được

\(A = \dfrac{{\sqrt {36}  - 1}}{{\sqrt {36}  - 3}}\) \( = \dfrac{{6 - 1}}{{6 - 3}} = \dfrac{5}{3}\)

Vậy với \(x = 36\) thì \(A = \dfrac{5}{3}\)

2) Rút gọn biểu thức B

Với \(x \ge 0;x \ne 1;x \ne 9\), ta có:

\(B = \dfrac{{\sqrt x  + 3}}{{\sqrt x  + 1}} - \dfrac{5}{{1 - \sqrt x }} + \dfrac{4}{{x - 1}}\)

\( = \dfrac{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}} + \dfrac{{5\left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\) \( + \dfrac{4}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\)

\( = \dfrac{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 1} \right) + 5\left( {\sqrt x  + 1} \right) + 4}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\)

\(\begin{array}{l} = \dfrac{{x + 2\sqrt x  - 3 + 5\sqrt x  + 5 + 4}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\ = \dfrac{{x + 7\sqrt x  + 6}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\ = \dfrac{{x + 6\sqrt x  + \sqrt x  + 6}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\ = \dfrac{{\sqrt x \left( {\sqrt x  + 6} \right) + \left( {\sqrt x  + 6} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\ = \dfrac{{\left( {\sqrt x  + 6} \right)\left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\\ = \dfrac{{\sqrt x  + 6}}{{\sqrt x  - 1}}\end{array}\)

Vậy \(B = \dfrac{{\sqrt x  + 6}}{{\sqrt x  - 1}}\)  với \(x \ge 0;x \ne 1;x \ne 9\)

3) Đặt \(P = A.B.\) Tìm \(x \in \mathbb{N}\) để P có giá trị lớn nhất

Với \(x \ge 0;x \ne 1;x \ne 9\), ta có:

\(P = A.B\) \( = \dfrac{{\sqrt x  - 1}}{{\sqrt x  - 3}}.\dfrac{{\sqrt x  + 6}}{{\sqrt x  - 1}}\) \( = \dfrac{{\sqrt x  + 6}}{{\sqrt x  - 3}} = \dfrac{{\sqrt x  - 3 + 9}}{{\sqrt x  - 3}}\)  \( = 1 + \dfrac{9}{{\sqrt x  - 3}}\)

Với \(0 \le x < 9\) thì \(\sqrt x  - 3 < 0\) \( \Rightarrow P = \dfrac{{\sqrt x  + 6}}{{\sqrt x  - 3}} < 0\)

Với \(x > 9\) mà \(x \in \mathbb{N}\) \( \Rightarrow x \ge 10\)

Suy ra \(\sqrt x  - 3 \ge \sqrt {10}  - 3 > 0\)

Do đó \(\dfrac{9}{{\sqrt x  - 3}} \le \dfrac{9}{{\sqrt {10}  - 3}}\)  nên \(1 + \dfrac{9}{{\sqrt x  - 3}} \le 1 + \dfrac{9}{{\sqrt {10}  - 3}}\)

Hay \(P \le 1 + \dfrac{9}{{\sqrt {10}  - 3}}\) 

Dấu “=” xảy ra khi \(x = 10\) (thỏa mãn điều kiện)

Vậy \(P\) đạt giá trị lớn nhất khi \(x = 10.\) 

LG bài 2

Phương pháp giải:

1) Diện tích xung quanh hình trụ có bán kính đáy \(r\) và chiều cao \(h\) là \({S_{xq}} = 2\pi rh\)

2) Giải bài toán bằng cách lập hệ phương trình 

B1: Chọn ẩn và đặt điều kiện cho ẩn

B2: Lập hệ phương trình và giải hệ phương trình

B3: So sánh điều kiện và kết luận

Lời giải chi tiết:

1) Khi uống trà sữa, người ta thường dùng ống hút bằng nhựa hình trụ có đường kính đáy 0,9cm, độ dài trục 21cm. Hỏi khi thải ra ngoài môi trường, diện tích nhựa gây ô nhiễm môi trường do 1000 ống hút gây ra là bao nhiêu?

Bán kính đáy ống hút là: \(0,9:2 = 0,45cm\)

Diện tích nhựa gây ô nhiễm do 1000 ống hút gây ra bằng với diện tích xung quanh của 1000 ống hút hình trụ có bán kính đáy 0,45cm và chiều cao 21cm.

Diện tích gây ô nhiễm cùa 1000 ống hút là: \(S = 1000.\left( {2\pi .0,45.21} \right)\) \( = 18900\pi \left( {c{m^2}} \right)\)

2) Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

Một người mua một cái bàn là và một cái quạt điện với tổng số tiền theo giá niêm yết là 850 nghìn đồng. Khi trả tiền người đó được khuyến mại giảm 20% đối với giá tiền bàn là và 10% đối với giá tiền quạt điện so với giá niêm yết. Vì vậy, người đó phải trả tổng cộng 740 nghìn đồng. Tính giá tiền của cái bàn là và cái quạt điện theo giá niêm yết.

Gọi giá tiền của 1 cái bàn là và 1 cái quạt điện lần lượt là \(x;y\) (nghìn đồng) \(\left( {0 < x,y < 840} \right)\)

Vì 1 cái bàn là và 1 cái quạt điện có tổng số tiền theo giá niêm yết là 850 nghìn đồng nên ta có phương trình:

\(x + y = 850\)  (1)

Thực tế, giá tiền 1 cái bàn là là: \(\left( {100\%  - 20\% } \right).x = 0,8x\) nghìn đồng

Thực tế, giá tiền 1 cái quạt điện là \(\left( {100\%  - 10\% } \right)y = 0,9y\) nghìn đồng

Vì thực tế người đó phải trả tổng cộng 740 nghìn đồng nên ta có phương trình:

\(0,8x + 0,9y = 740\) (2)

Từ (1) và (2) ta có hệ phương trình:

\(\left\{ \begin{array}{l}x + y = 850\\0,8x + 0,9y = 740\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}0,8x + 0,8y = 680\\0,8x + 0,9y = 740\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0,1y = 60\\x + y = 850\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 600\\x + 600 = 850\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}y = 600\left( {tm} \right)\\x = 250\left( {tm} \right)\end{array} \right.\end{array}\)

Vậy giá tiền niêm yết của 1 cái bàn là là 250 nghìn đồng 

Giá niêm yết của 1 cái quạt điện là 600 nghìn đồng.

LG bài 3

Phương pháp giải:

1) Giải hệ phương trình bằng phương pháp cộng đại số

2) Phương trình \(a{x^4} + b{x^2} + c = 0\) có ba nghiệm phân biệt thì trong ba nghiệm đó có 1 nghiệm \(x = 0.\) Thay \(x = 0\) vào phương trình để tìm \(m,\) sau đó thử lại xem phương trình có đủ 3 nghiệm với m vừa tìm được hay không.

Lời giải chi tiết:

1) Giải hệ phương trình \(\left\{ \begin{array}{l}2\sqrt {x - 2}  + \sqrt {y - 1}  = 5\\\sqrt {x - 2}  + \sqrt {y - 1}  = 3\end{array} \right.\)

Điều kiện: \(x \ge 2;y \ge 1\)

\(\left\{ \begin{array}{l}2\sqrt {x - 2}  + \sqrt {y - 1}  = 5\\\sqrt {x - 2}  + \sqrt {y - 1}  = 3\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}\sqrt {x - 2}  = 2\\\sqrt {x - 2}  + \sqrt {y - 1}  = 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x - 2 = 4\\2 + \sqrt {y - 1}  = 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 6\\\sqrt {y - 1}  = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 6\\y - 1 = 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 6\left( {tm} \right)\\y = 2\left( {tm} \right)\end{array} \right.\end{array}\)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {6;2} \right)\)

2) Cho phương trình \({x^4} - 2m{x^2} + {m^2} - 4 = 0\) (*)

a) Giải phương trình với \(m = 3.\)

Thay \(m = 3\) vào phương trình (*) ta được:

\(\begin{array}{l}{x^4} - 6{x^2} + 5 = 0\\ \Leftrightarrow {x^4} - 5{x^2} - {x^2} + 5 = 0\\ \Leftrightarrow {x^2}\left( {{x^2} - 5} \right) - \left( {{x^2} - 5} \right) = 0\\ \Leftrightarrow \left( {{x^2} - 1} \right)\left( {{x^2} - 5} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{x^2} = 1\\{x^2} = 5\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x =  \pm 1\\x =  \pm \sqrt 5 \end{array} \right.\end{array}\)

Vậy phương trình đã cho có tập nghiệm \(S = \left\{ { \pm 1; \pm \sqrt 5 } \right\}\) với \(m = 3.\)

b) Tìm m để phương trình có 3 nghiệm phân biệt

Đặt \({x^2} = t\left( {t \ge 0} \right)\) ta có phương trình:

\({t^2} - 2mt + {m^2} - 4 = 0\) (1)

Để phương trình (*) có 3 nghiệm phân biệt thì phương trình (1) có 1 nghiệm \({t_1} = 0\) và một ngiệm \({t_2} > 0\)

Thay \(t = 0\) vào phương trình (1) ta được: \({m^2} - 4 = 0 \Leftrightarrow {m^2} = 4\) \( \Leftrightarrow \left[ \begin{array}{l}m = 2\\m =  - 2\end{array} \right.\) 

Với \(m =  - 2\) ta có phương trình \({t^2} + 2t = 0 \Leftrightarrow t\left( {t + 2} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}t = 0\\t =  - 2\end{array} \right.\) (loại vì \(t =  - 2 < 0\))

Với \(m = 2\) ta có phương trình \({t^2} - 2t = 0 \Leftrightarrow t\left( {t - 2} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 2\end{array} \right.\) (thỏa mãn)

Vậy với \(m = 2\) thì phương trình đã cho có 3 nghiệm phân biệt.

LG bài 4

Phương pháp giải:

1) Chứng minh tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.

2) Chứng minh 2 vé của đẳng thức đều bằng \(A{C^2}\).

3) Chứng minh \(\widehat {HOE} + \widehat {EDH} = {180^0}\) suy ra tứ giác nội tiếp.

Chứng minh tỉ lệ \(\dfrac{{DI}}{{BE}} = \dfrac{{DK}}{{BE}}\) suy ra \(DI = DK\).

Lời giải chi tiết:

Từ điểm A ở ngoài đường tròn \(\left( {O;R} \right)\) vẽ hai tiếp tuyến AB, AC (B, C là các tiếp điểm) và cát tuyến ADE thuộc nửa mặt phẳng bờ là đường thẳng OA không chứa điểm B của đường tròn (O). Gọi H là giao điểm của OA và BC. 

1) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn

Ta có:

AB là tiếp tuyến với đường tròn nên \(AB \bot OB \Rightarrow \widehat {ABO} = {90^0}\) (tính chất)

AC là tiếp tuyến với đường tròn nên \(AC \bot OC \Rightarrow \widehat {ACO} = {90^0}\) (tính chất)

Tứ giác ABOC có:

\(\widehat {ABO} + \widehat {ACO}\) \( = {90^0} + {90^0} = {180^0}\)

Do đó ABOC là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp)

Vậy bốn điểm A, B, O, C cùng thuộc một đường tròn (đpcm).

2) Chứng minh \(AO \bot BC\) tại H và \(AH.AO = AD.AE\)

AB, AB là tiếp tuyến với đường tròn nên AB=AC (tính chất)

Lại có OB=OC (bán kính)

\( \Rightarrow OA\) là đường trung trực của BC

\( \Rightarrow OA \bot BC\) tại trung điểm \(H\). 

Xét tam giác \(ACD\) và \(AEC\) có:

\(\widehat {ACD} = \widehat {AEC}\) (góc giữa tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(CD\))

\(\widehat A\) chung

\( \Rightarrow \Delta ACD \backsim \Delta AEC\left( {g - g} \right)\)

\( \Rightarrow \dfrac{{AC}}{{AE}} = \dfrac{{AD}}{{AC}}\) (cạnh tương ứng)

\( \Rightarrow A{C^2} = AD.AE\) (1)

Tam giác ACO vuông tại C có CH là đường cao nên \(AH.AO = A{C^2}\) (2) (hệ thức giữa cạnh và đường cao trong tam giác)

Từ (1) và (2) suy ra \(AD.AE = AH.AO\left( { = A{C^2}} \right)\) (đpcm).

3) Đường thẳng đi qua điểm D và song song với đường thẳng BE cắt AB, BC lần lượt tại I, K. Chứng minh tứ giác OHDE nội tiếp và D là trung điểm của IK.

*) Chứng minh DHOE nội tiếp.

Từ câu b, \(AD.AE = AH.AO\) \( \Rightarrow \dfrac{{AD}}{{AO}} = \dfrac{{AH}}{{AE}}\)

Xét \(\Delta ADH\) và \(\Delta AOE\) có:

\(\begin{array}{l}\dfrac{{AD}}{{AO}} = \dfrac{{AH}}{{AE}}\,\,\left( {cmt} \right)\\\widehat A\,\,\,chung\\ \Rightarrow \Delta ADH \backsim \Delta AOE\left( {c - g - c} \right)\end{array}\)

\( \Rightarrow \widehat {ADH} = \widehat {AOE}\) (góc tương ứng)

Mà \(\widehat {ADH} + \widehat {EDH} = {180^0}\) (kề bù)

\( \Rightarrow \widehat {AOE} + \widehat {EDH} = {180^0}\) hay \(\widehat {HOE} + \widehat {EDH} = {180^0}\)

\( \Rightarrow DHOE\) nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\))

*) Chứng minh D là trung điểm của IK.

Ta có: \(\Delta ADH \backsim \Delta AOE\) \( \Rightarrow \widehat {AHD} = \widehat {AEO} = \widehat {DEO}\) (3)

Tứ giác DHOE nội tiếp nên \(\widehat {EDO} = \widehat {EHO}\) (cùng chắn cung \(DO\)) (4)

Tam giác DOE có \(OD = OE\) nên là tam giác cân

\( \Rightarrow \widehat {EDO} = \widehat {DEO}\) (5)

Từ (3), (4) và (5) suy ra \(\widehat {EHO} = \widehat {AHD}\)

Gọi M là giao điểm của DE và BC ta có:

\(\begin{array}{l}\widehat {AHD} + \widehat {DHM} = \widehat {AHM} = {90^0}\\\widehat {EHO} + \widehat {EHM} = \widehat {OHM} = {90^0}\end{array}\)

\( \Rightarrow \widehat {DHM} = \widehat {EHM}\) (do \(\widehat {EHO} = \widehat {AHD}\))

\( \Rightarrow HM\) là tia phân giác của góc \(\widehat {DHE}\)

\( \Rightarrow \dfrac{{MD}}{{ME}} = \dfrac{{HD}}{{HE}}\) (tính chất đường phân giác)

Lại có, \(HA \bot HM\) nên \(HA\) là phân giác ngoài của góc \(\widehat {DHM}\))

\( \Rightarrow \dfrac{{AD}}{{AE}} = \dfrac{{HD}}{{HE}}\) (tính chất đường phân giác ngoài goác \(\widehat {DHM}\))

Do đó \(\dfrac{{MD}}{{ME}} = \dfrac{{AD}}{{AE}}\left( { = \dfrac{{HD}}{{HE}}} \right)\) (6)

DI//BE\( \Rightarrow \dfrac{{DI}}{{BE}} = \dfrac{{AD}}{{AE}}\) (Ta-let)

DK//BE\( \Rightarrow \dfrac{{DK}}{{BE}} = \dfrac{{MD}}{{ME}}\) (Ta-let)

Do (6) nên \(\dfrac{{DI}}{{BE}} = \dfrac{{DK}}{{BE}} \Rightarrow DI = DK\)

Vậy D là trung điểm của IK.

LG bài 5

Phương pháp giải:

Ta chứng minh \(\dfrac{{{x^3} + {y^3}}}{{{x^2} + {y^2}}} \ge \dfrac{1}{2}\left( {x + y} \right)\)

Áp dụng tương tự với các phân thức còn lại để đánh giá tìm giá trị nhỏ nhất của \(P.\)

Lời giải chi tiết:

Cho ba số thực \(x,y,z > 0\) thỏa mãn \(x + y + z \ge 6.\)

Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^3} + {y^3}}}{{{x^2} + {y^2}}} + \dfrac{{{y^3} + {z^3}}}{{{y^2} + {z^2}}}\) \( + \dfrac{{{z^3} + {x^3}}}{{{z^2} + {x^2}}}\)

Ta chứng minh \(\dfrac{{{x^3} + {y^3}}}{{{x^2} + {y^2}}} \ge \dfrac{1}{2}\left( {x + y} \right)\)

Thật vậy, ta có:

\(\dfrac{{{x^3} + {y^3}}}{{{x^2} + {y^2}}} \ge \dfrac{1}{2}\left( {x + y} \right)\)

\( \Leftrightarrow 2\left( {{x^3} + {y^3}} \right) \ge \left( {x + y} \right)\left( {{x^2} + {y^2}} \right)\)  (vì \({x^2} + {y^2} > 0\))

\( \Leftrightarrow 2\left( {x + y} \right)\left( {{x^2} - xy + {y^2}} \right)\) \( - \left( {x + y} \right)\left( {{x^2} + {y^2}} \right) \ge 0\)

\( \Leftrightarrow \left( {x + y} \right)\left( {2{x^2} - 2xy + 2{y^2} - {x^2} - {y^2}} \right) \ge 0\)

\( \Leftrightarrow \left( {x + y} \right)\left( {{x^2} - 2xy + {y^2}} \right) \ge 0\)

\( \Leftrightarrow \left( {x + y} \right){\left( {x - y} \right)^2} \ge 0\) (luôn đúng với mọi \(x,y > 0\))

Vậy  \(\dfrac{{{x^3} + {y^3}}}{{{x^2} + {y^2}}} \ge \dfrac{1}{2}\left( {x + y} \right)\)

Tương tự ta có \(\dfrac{{{y^3} + {z^3}}}{{{y^2} + {z^2}}} \ge \dfrac{1}{2}\left( {y + z} \right)\) và \(\dfrac{{{x^3} + {z^3}}}{{{x^2} + {z^2}}} \ge \dfrac{1}{2}\left( {x + z} \right)\)

Suy ra \(\dfrac{{{x^3} + {y^3}}}{{{x^2} + {y^2}}} + \dfrac{{{y^3} + {z^3}}}{{{y^2} + {z^2}}} + \dfrac{{{x^3} + {z^3}}}{{{x^2} + {z^2}}}\) \( \ge \dfrac{1}{2}\left( {x + y} \right)\)\( + \dfrac{1}{2}\left( {y + z} \right) + \dfrac{1}{2}\left( {x + z} \right)\)

\(\begin{array}{l} \Leftrightarrow P \ge \dfrac{1}{2}\left( {2x + 2y + 2z} \right)\\ \Leftrightarrow P \ge x + y + z \ge 6\\ \Leftrightarrow P \ge 6\end{array}\)

Dấu “=” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}x = y\\y = z\\x = z\\x + y + z = 6\end{array} \right.\) \( \Leftrightarrow x = y = z = 2\)

Vậy giá trị nhỏ nhất của \(P\) là \(6\) khi \(x = y = z = 2\).

HẾT

 Loigiaihay.com