Đề kiểm tra học kì 1 Toán 9 - Đề số 25

Đề bài

Câu 1: (1,5 điểm) Tính:

a) \(\sqrt {15 - 6\sqrt 6 }  + \sqrt {33 - 12\sqrt 6 } \).

b) \(\frac{2}{{\sqrt 5  - 2}} + \frac{{3\sqrt 5  - 5}}{{\sqrt 5  - 3}} - 5\sqrt {\frac{1}{5}} \)

Câu 2: (1,5 điểm) Cho hàm số \(y = \frac{1}{2}x + 2\) có đồ thị (D₁) và \(y =  - x + 3\) có đồ thị (D₂).

a) Vẽ đồ thị (D₁) và (D₂) trên cùng một hệ trục tọa độ

b) Tìm tọa độ giao điểm  của (D₁) và (D₂) bằng phép  tính.

Câu 3: (1 điểm) Giải phương trình: \(\;\sqrt {{x^2} - 8x + 16}  = 3x - 1\)

Câu 4: (1 điểm) Một học sinh đứng ở mặt đất cách tháp ăng-ten cao 150m nhìn thấy đỉnh tháp theo một góc nghiêng lên là 20⁰ và khoảng cách từ  mắt đến mặt đất là 1m.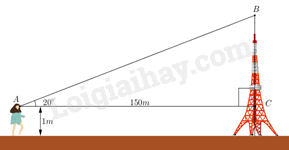

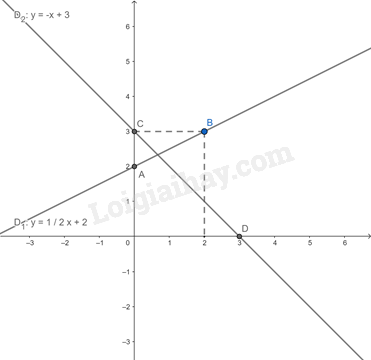
Tính chiều cao của tháp (làm tròn đến mét)

Câu 5: (1 điểm) Nhiệt độ ở mặt đất đo được khoảng 30⁰C. Biết rằng cứ lên 1km thì nhiệt độ giảm đi 5⁰C .

a) Hãy lập hàm số T theo h, trong đó T tính bằng độ (⁰C ) và h là độ cao so với mặt đất tính bằng ki-lô-mét (km)

b) Hãy tính nhiệt độ khi ở độ cao 3km so với mặt đất.

Câu 6: (1 điểm) Tại siêu thị Điện Máy Xanh có chương trình khuyến mãi giảm giá so với giá niêm yết như sau: quạt máy giảm giá 10%; tivi giảm giá 20%; tủ lạnh giảm giá 15%. Anh Minh đã đến siêu thị trên mua 1 quạt máy, 1 tivi, 1 tủ lạnh với tổng số tiền trả là 24590000 đồng. Biết giá niêm yết của 1 quạt máy và 1 tivi lần lượt là 600000 đồng và 12000000 đồng. Tính giá niêm yết của chiếc tủ lạnh anh Minh đã mua.

Câu 7: (3 điểm) Cho đường tròn (O; R) đường kính AB và một điểm C nằm trên đường tròn (O) sao cho AC < BC. Tiếp tuyến tại B của (O) cắt tia AC tại M.

a) Chứng minh \(\Delta \)ABC vuông và AC.AM = 4R².

b) Tiếp tuyến tại C của (O) cắt MB tại E. Chứng minh OE // AM.

c) AE cắt (O) tại K. Chứng minh \(\widehat {AKC} = \widehat {AME}\).

-------- Hết --------

Lời giải

Câu 1: (1,5 điểm) Tính:

a) \(\sqrt {15 - 6\sqrt 6 }  + \sqrt {33 - 12\sqrt 6 } \).

b) \(\frac{2}{{\sqrt 5  - 2}} + \frac{{3\sqrt 5  - 5}}{{\sqrt 5  - 3}} - 5\sqrt {\frac{1}{5}} \).

Phương pháp

Sử dụng công thức khai phương căn bậc hai, trục căn thức.

Lời giải

a) \(\sqrt {15 - 6\sqrt 6 }  + \sqrt {33 - 12\sqrt 6 } \)

\( = 3 - \sqrt 6  + 2\sqrt 6  - 3\)

\( = \sqrt 6 \)                                                       

b)\(\frac{2}{{\sqrt 5  - 2}} + \frac{{3\sqrt 5  - 5}}{{\sqrt 5  - 3}} - 5\sqrt {\frac{1}{5}} \)

\( = \frac{{2\left( {\sqrt 5  + 2} \right)}}{{5 - {2^2}}} + \frac{{\sqrt 5 \left( {3 - \sqrt 5 } \right)}}{{\sqrt 5  - 3}} - \frac{5}{{\sqrt 5 }}\)

\( = 2\left( {\sqrt 5  + 2} \right) - \sqrt 5  - \sqrt 5 \)

\( = 4\)                       

Câu 2: (1,5 điểm) Cho hàm số \(y = \frac{1}{2}x + 2\) có đồ thị (D₁) và \(y =  - x + 3\) có đồ thị (D₂).

a) Vẽ đồ thị (D₁) và (D₂) trên cùng một hệ trục tọa độ

b) Tìm tọa độ giao điểm  của (D₁) và (D₂) bằng phép  tính.

Phương pháp

a) Lấy hai điểm thuộc đồ thị hàm số, ta được đồ thị của hàm số đó.

b) Viết phương trình hoành độ giao điểm của (D₁) và (D₂). Tìm nghiệm của phương trình. Thay giá trị x tìm được để tìm y.

Lời giải

a) Ta thấy:

+) \(A\left( {0;2} \right),B\left( {2;3} \right)\) thuộc đồ thị hàm số \(y = \frac{1}{2}x + 2\).

+) \(C\left( {0;3} \right);D\left( {3;0} \right)\) thuộc đồ thị hàm số \(y =  - x + 3\).

Từ đó ta có đồ thị của hai hàm số:

b) Ta có phương trình hoành độ giao điểm của hai đường thẳng (D₁) và (D₂) là:

\(\begin{array}{l}\frac{1}{2}x + 2 =  - x + 3\\\frac{1}{2}x + x = 3 - 2\\\frac{3}{2}x = 1\\x = \frac{2}{3}\end{array}\)

Với \(x = \frac{2}{3}\) ta có \(y =  - \frac{2}{3} + 3 = \frac{7}{3}\) ta được điểm \(G\left( {\frac{2}{3};\frac{7}{3}} \right)\).

Vậy giao điểm của (D₁) và (D₂) là điểm \(G\left( {\frac{2}{3};\frac{7}{3}} \right)\).

Câu 3: (1 điểm) Giải phương trình: \(\;\sqrt {{x^2} - 8x + 16}  = 3x - 1\)

Phương pháp

Bình phương hai vế để tìm x.

Lời giải

\(\;\sqrt {{x^2} - 8x + 16}  = 3x - 1\)

\( \Leftrightarrow \left| {x - 4} \right| = 3x - 1\;\;\) (ĐK: \(x \ge \frac{1}{3}\))

\( \Leftrightarrow \left[ \begin{array}{l}x - 4 = 3x - 1\\x - 4 =  - 3x + 1\end{array} \right.\)

\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{{ - 3}}{2}(kTM)\\x = \;\frac{5}{4}\left( {TM} \right)\end{array} \right.\)

Vậy nghiệm của phương trình là \(x = \;\frac{5}{4}\).

Câu 4: (1 điểm) Một học sinh đứng ở mặt đất cách tháp ăng-ten cao 150m nhìn thấy đỉnh tháp theo một góc nghiêng lên là 20⁰ và khoảng cách từ  mắt đến mặt đất là 1m.

Tính chiều cao của tháp (làm tròn đến mét)

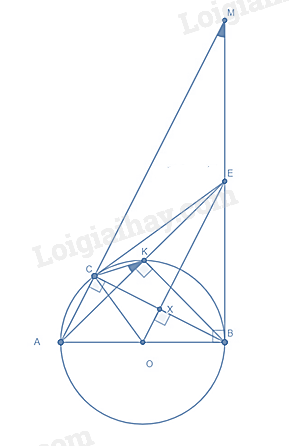
Phương pháp

Sử dụng tỉ số lượng giác của góc nhọn.

Lời giải

Xét tam giác ABC vuông tại C, ta có:

            \({\rm{BC}} = {\rm{AC}}.\tan \widehat {{\rm{BAC}}} = 150.{\rm{tan}}{20^0} \approx 55\left( {\rm{m}} \right)\)

Vậy chiều cao AH của tháp khoảng 56m.

Câu 5: (1 điểm) Nhiệt độ ở mặt đất đo được khoảng 30⁰C. Biết rằng cứ lên 1km thì nhiệt độ giảm đi 5⁰C .

a) Hãy lập hàm số T theo h, trong đó T tính bằng độ (⁰C ) và h là độ cao so với mặt đất tính bằng ki-lô-mét (km)

b) Hãy tính nhiệt độ khi ở độ cao 3km so với mặt đất.

Phương pháp

a) Lập hàm số dựa vào dữ kiện đề bài.

b) Thay h = 3 vào để tính.

Lời giải

a) Nhiệt độ ở mặt đấy đo được khoảng 30⁰C.

Vì cứ lên 1km thì nhiệt độ giảm đi 5⁰C nên lên h km thì nhiệt độ giảm đi 5.h (⁰C)

=> Ta có hàm số: T = 30 – 5h

b) Thay h = 3 vào hàm số T = 30 – 5h, ta được:

T = 30 – 5.3 = 15 (⁰C)

Câu 6: (1 điểm) Tại siêu thị Điện Máy Xanh có chương trình khuyến mãi giảm giá so với giá niêm yết như sau: quạt máy giảm giá 10%; tivi giảm giá 20%; tủ lạnh giảm giá 15%. Anh Minh đã đến siêu thị trên mua 1 quạt máy, 1 tivi, 1 tủ lạnh với tổng số tiền trả là 24590000 đồng. Biết giá niêm yết của 1 quạt máy và 1 tivi lần lượt là 600000 đồng và 12000000 đồng. Tính giá niêm yết của chiếc tủ lạnh anh Minh đã mua.

Phương pháp

Tính số tiền anh Minh mua quạt máy, số tiền anh Minh mua tivi => giá tiền anh Minh mua tủ lạnh.

Tính giá niêm yết của chiếc tủ lạnh.

Lời giải

Số tiền anh Minh mua quạt máy là: 600 000.(100% - 10%) = 540 000 (đồng).

Số tiền anh Minh mua ti vi là: 12 000 000.(100% - 20%) = 9 600 000 (đồng).

Số tiền anh Minh mua tủ lạnh là: 24 590 000 – 540 000 – 9 600 000 = 14 450 000 (đồng).

Giá niêm yết của chiếc tủ lạnh anh Minh đã mua là: 14 450 000 : (100% - 15%) = 17 000 000 (đồng)

Câu 7: (3 điểm) Cho đường tròn (O; R) đường kính AB và một điểm C nằm trên đường tròn (O) sao cho AC < BC. Tiếp tuyến tại B của (O) cắt tia AC tại M.

a) Chứng minh \(\Delta \)ABC vuông và AC.AM = 4R².

b) Tiếp tuyến tại C của (O) cắt MB tại E. Chứng minh OE // AM.

c) AE cắt (O) tại K. Chứng minh \(\widehat {AKC} = \widehat {AME}\).

Phương pháp

a) Ta có : AB = AC ; OB = OC
Suy ra OA là đường trung trực của BC
Suy ra OA vuông góc BC

b) Chứng minh OE là đường trung trực của BC \( \Rightarrow \) OE \( \bot \) BC \( \Rightarrow \) OE // AM

c) Chứng minh: \(\Delta \)AKB vuông tại K

Chứng minh AC.AM = AK.AE \( \Rightarrow \) \(\Delta \)AKC $\backsim $ \(\Delta \)AME \( \Rightarrow \) đpcm

Lời giải

a) Ta có : \(\Delta ABC\prime \) nội tiếp \((O;R)\) (Do \(\left. {A,B,C\prime  \in (O)} \right)\)

Mà AB là đường kính của \((O;R)\)

\( \Rightarrow \Delta ABC\) vuông tại C

\( \Rightarrow BC \bot AM\) tại C \((BC \bot AC;\overline {A,C,M} )\)

Xét  \(\Delta AMB\) vuông tại \(B\), đường cao BC có :

\(A{B^2} = AC \cdot AM\) (hệ thức lượng)

\( \Rightarrow {(2R)^2} = AC \cdot AM\)

\( \Rightarrow AC \cdot AM = 4{R^2}\)

b) Gọi X là giao điểm của OE và BC

Khi đó \(BC \bot OE\) tại \(X\)

Mà \(BC \bot AC\) tại \(C(\Delta ABC\) vuông tại \(C)\)

\( \Rightarrow OE//AC\)

Mà \(\overline {A,C,M} \)

\( \Rightarrow OE//AM\)

c) Ta có : \(\Delta AKB\) nội tiếp \((O;R)\) ( Do \(A,B,K \in (O;R))\)

Mà AB là đường kính (gt) \( \Rightarrow \Delta AKB\) vuông tại \(K\)

\( \Rightarrow BK \bot AE\) tại K \((BK \bot AK;\overline {A,K,E} )\)

Xét \(\Delta ABE\) vuông tại \(B\), đường cao BK có : \(A{B^2} = AK \cdot AE\) ( Hệ thức lượng )

Mà \(A{B^2} = AC \cdot AM(cmt)\)

\( \Rightarrow AK \cdot KE = AC \cdot AM\)

\( \Rightarrow \frac{{AK}}{{AM}} = \frac{{AC}}{{AE}}\)

Mà \(\widehat {MAE}\) chung

$\Delta A K C \backsim \Delta A M E(c-g-c)$

\( \Rightarrow \widehat {AKC} = \widehat {AME}\)