Lý thuyết Tích vô hướng của hai vecto - SGK Toán 10 Kết nối tri thức

1. GÓC GIỮA HAI VECTO

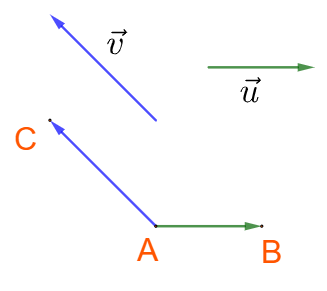
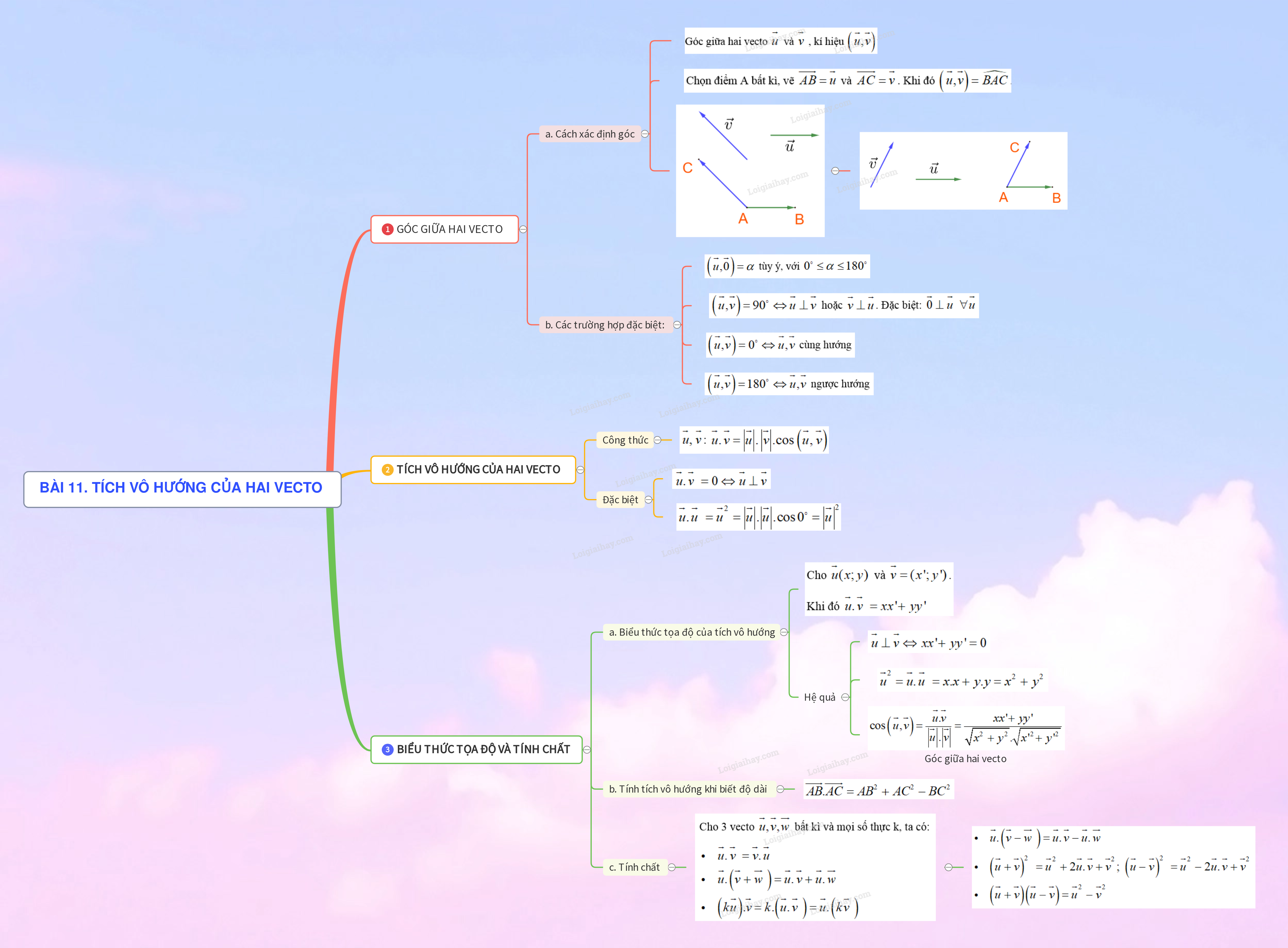
Cho hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) khác \(\overrightarrow 0 \). Góc giữa hai vecto \(\overrightarrow u \) và \(\overrightarrow v \) , kí hiệu \(\left( {\;\overrightarrow u ,\overrightarrow v } \right)\)

a) Cách xác định góc: Chọn điểm A bất kì, vẽ \(\overrightarrow {AB}  = \overrightarrow u \) và \(\overrightarrow {AC}  = \overrightarrow v \). Khi đó \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = \widehat {BAC}\).

b) Các trường hợp đặc biệt:

+) \(\left( {\;\overrightarrow u ,\overrightarrow 0 } \right) = \alpha \) tùy ý, với \({0^ \circ } \le \alpha  \le {180^ \circ }\)

+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {90^ \circ } \Leftrightarrow \overrightarrow u  \bot \overrightarrow v \) hoặc \(\overrightarrow v  \bot \overrightarrow u \). Đặc biệt: \(\overrightarrow 0  \bot \overrightarrow u \;\;\forall \overrightarrow u \;\)

+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {0^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) cùng hướng

+) \(\left( {\;\overrightarrow u ,\overrightarrow v } \right) = {180^ \circ } \Leftrightarrow \overrightarrow u ,\overrightarrow v \) ngược hướng

2. TÍCH VÔ HƯỚNG CỦA HAI VECTO

+) Tích vô hướng của hai vecto \(\overrightarrow u ,\;\overrightarrow v \): \(\overrightarrow u .\;\overrightarrow v  = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)

+) \(\overrightarrow u .\;\overrightarrow v \;\; = 0 \Leftrightarrow \overrightarrow u  \bot \;\overrightarrow v \;\;\)

+) \(\overrightarrow u .\;\overrightarrow u \;\; = {\overrightarrow u ^2} = \left| {\overrightarrow u } \right|.\left| {\overrightarrow u } \right|.\cos {0^ \circ } = {\left| {\overrightarrow u } \right|^2}\)

3. BIỂU THỨC TỌA ĐỘ VÀ TÍNH CHẤT CỦA TÍCH VÔ HƯỚNG

a) Biểu thức tọa độ của tích vô hướng

Cho \(\overrightarrow u (x;y)\) và \(\overrightarrow v  = (x';y')\).

Khi đó \(\overrightarrow u .\;\overrightarrow v \;\; = xx' + yy'\)

Hệ quả:

+) \(\overrightarrow u  \bot \;\overrightarrow v \; \Leftrightarrow xx' + yy' = 0\)

+) \({\overrightarrow u ^2} = \overrightarrow u .\;\overrightarrow u \;\; = x.x + y.y = {x^2} + {y^2}\)

+) Tìm góc giữa hai vecto: \(\cos \left( {\;\overrightarrow u ,\overrightarrow v } \right) = \frac{{\;\overrightarrow u .\overrightarrow v }}{{\;\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}} = \frac{{xx' + yy'}}{{\sqrt {{x^2} + {y^2}} .\sqrt {x{'^2} + y{'^2}} }}\)

b) Công thức tính tích vô hướng khi biết độ dài:

Theo định lí cosin: \(\cos \widehat {BAC} = \frac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}\)

\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC}  = AB.AC.\cos \widehat {BAC} = A{B^2} + A{C^2} - B{C^2}\)

 c) Tính chất

Cho 3 vecto \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w \) bất kì và mọi số thực k, ta có:

\(\begin{array}{l}\overrightarrow u .\;\overrightarrow v \;\; = \overrightarrow v .\;\overrightarrow u \;\\\overrightarrow u .\;\left( {\overrightarrow v  + \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; + \overrightarrow u .\;\overrightarrow w \;\\\left( {k\overrightarrow u } \right).\overrightarrow v  = k.\left( {\overrightarrow u .\;\overrightarrow v \;} \right) = \overrightarrow u .\;\left( {k\overrightarrow v \;} \right)\end{array}\)

Hệ quả

\(\begin{array}{l}\overrightarrow u .\;\left( {\overrightarrow v  - \overrightarrow w \;} \right)\; = \overrightarrow u .\;\overrightarrow v \; - \overrightarrow u .\;\overrightarrow w \\{\left( {\overrightarrow u  + \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} + 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2};\;\;{\left( {\overrightarrow u  - \overrightarrow v } \right)^2}\;\; = {\overrightarrow u ^2} - 2\overrightarrow u .\;\overrightarrow v \; + \;{\overrightarrow v ^2}\\\left( {\overrightarrow u  + \overrightarrow v } \right)\left( {\overrightarrow u  - \overrightarrow v } \right) = {\overrightarrow u ^2} - {\overrightarrow v ^2}\end{array}\)