Giải mục 3 trang 68, 69, 70 SGK Toán 10 tập 1 - Kết nối tri thức

HĐ2

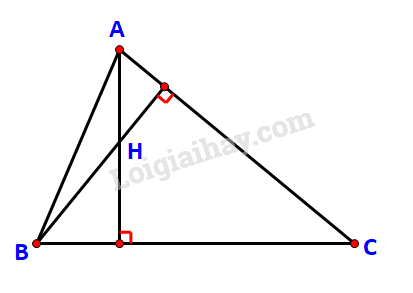
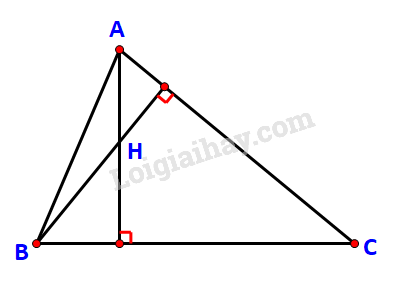
Cho hai vectơ cùng phương \(\overrightarrow u  = \left( {x;y} \right)\) và \(\overrightarrow v  = \left( {kx;ky} \right)\). Hãy kiểm tra công thức \(\overrightarrow u .\overrightarrow v  = k\left( {{x^2} + {y^2}} \right)\) theo từng trường hợp sau:

a) \(\overrightarrow u  = \overrightarrow 0 \)

b) \(\overrightarrow u  \ne \overrightarrow 0 \) và \(k \ge 0\)

c) \(\overrightarrow u  \ne \overrightarrow 0 \) và \(k < 0\)

Phương pháp giải:

Tính tích vô hướng bằng công thức: \(\overrightarrow u .\;\overrightarrow v  = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right|.\cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right)\)

Lời giải chi tiết:

a) Vì \(\overrightarrow u  = \overrightarrow 0 \) nên \(\overrightarrow u \) vuông góc với mọi \(\overrightarrow v \).

Như vậy \(\overrightarrow u .\overrightarrow v  = 0\)

Mặt khác: \(\overrightarrow u  = \overrightarrow 0  \Leftrightarrow x = y = 0\)

\( \Rightarrow k\left( {{x^2} + {y^2}} \right) = 0 = \overrightarrow u .\overrightarrow v \)

b) Vì \(\overrightarrow u  \ne \overrightarrow 0 \) và \(k \ge 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \)cùng hướng.

\( \Rightarrow \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {0^o} \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = 1\)

\(\begin{array}{l} \Rightarrow \overrightarrow u .\;\overrightarrow v  = \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| = \sqrt {{x^2} + {y^2}} .\sqrt {{{\left( {kx} \right)}^2} + {{\left( {ky} \right)}^2}} \\ = \sqrt {{x^2} + {y^2}} .\left| k \right|.\sqrt {{x^2} + {y^2}}  = k\left( {{x^2} + {y^2}} \right)\end{array}\)

(|k|= k do k > 0)

c) Vì \(\overrightarrow u  \ne \overrightarrow 0 \) và \(k < 0\) nên \(\overrightarrow u \) và \(\overrightarrow v \)ngược hướng.

\( \Rightarrow \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) = {180^o} \Leftrightarrow \cos \;\left( {\overrightarrow u ,\;\overrightarrow v } \right) =  - 1\)

\(\begin{array}{l} \Rightarrow \overrightarrow u .\;\overrightarrow v  =  - \left| {\overrightarrow u } \right|.\;\left| {\overrightarrow v } \right| =  - \sqrt {{x^2} + {y^2}} .\sqrt {{{\left( {kx} \right)}^2} + {{\left( {ky} \right)}^2}} \\ =  - \sqrt {{x^2} + {y^2}} .\left| k \right|.\sqrt {{x^2} + {y^2}}  = k\left( {{x^2} + {y^2}} \right).\end{array}\)

HĐ3

Trong mặt phẳng tọa độ Oxy, cho hai vectơ không cùng phương \(\overrightarrow u  = \left( {x;y} \right)\) và \(\overrightarrow v  = \left( {x';y'} \right)\).

a) Xác định tọa độ của các điểm A và B sao cho \(\overrightarrow {OA}  = \overrightarrow u ,\;\overrightarrow {OB}  = \overrightarrow v .\)

b) Tính \(A{B^2},O{A^2},O{B^2}\) theo tọa độ của A và B.

c) Tính \(\overrightarrow {OA} .\overrightarrow {OB} \) theo tọa độ của A, B.

Lời giải chi tiết:

a) Vì \(\overrightarrow {OA}  = \overrightarrow u  = (x;y)\) nên A(x; y).

Tương tự: do \(\overrightarrow {OB}  = \overrightarrow v  = \left( {x';y'} \right)\) nên B (x’; y’)

b) Ta có: \(\overrightarrow {OA}  = (x;y) \Rightarrow O{A^2} = {\left| {\overrightarrow {OA} } \right|^2} = {x^2} + {y^2}.\)

Và \(\overrightarrow {OB}  = (x';y') \Rightarrow O{B^2} = {\left| {\overrightarrow {OB} } \right|^2} = x{'^2} + y{'^2}.\)

Lại có: \(\overrightarrow {AB}  = \overrightarrow {OB}  - \overrightarrow {OA}  = \left( {x';y'} \right) - \left( {x;y} \right) = \left( {x' - x;y' - y} \right)\)

\( \Rightarrow A{B^2} = {\left| {\overrightarrow {AB} } \right|^2} = {\left( {x' - x} \right)^2} + {\left( {y' - y} \right)^2}.\)

c) Theo định lí cosin trong tam giác OAB ta có:

\(\cos \widehat O = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}}\)

Mà \(\overrightarrow {OA} .\overrightarrow {OB}  = \left| {\overrightarrow {OA} } \right|.\left| {\overrightarrow {OB} } \right|.\cos \left( {\overrightarrow {OA} ,\overrightarrow {OB} } \right) = OA.OB.\cos \widehat O\)

\( \Rightarrow \overrightarrow {OA} .\overrightarrow {OB}  = OA.OB.\frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}} = \frac{{O{A^2} + O{B^2} - A{B^2}}}{2}\)

\(\begin{array}{l} \Rightarrow \overrightarrow {OA} .\overrightarrow {OB}  = \frac{{{x^2} + {y^2} + x{'^2} + y{'^2} - {{\left( {x' - x} \right)}^2} - {{\left( {y' - y} \right)}^2}}}{2}\\ \Leftrightarrow \overrightarrow {OA} .\overrightarrow {OB}  = \frac{{ - \left( { - 2x'.x} \right) - \left( { - 2y'.y} \right)}}{2} = x'.x + y'.y\end{array}\)

Luyện tập 3

Tích vô hướng và góc giữa hai vectơ \(\overrightarrow u  = \left( {0; - 5} \right),\;\overrightarrow v  = \left( {\sqrt 3 ;1} \right)\)

Phương pháp giải:

Cho \(\overrightarrow u  = \left( {x;y} \right)\) và \(\overrightarrow v  = \left( {x';y'} \right)\), khi đó: \(\overrightarrow u .\overrightarrow v  = x.x' + y.y'\)

Lời giải chi tiết:

 Ta có: \(\overrightarrow u  = \left( {0; - 5} \right),\;\overrightarrow v  = \left( {\sqrt 3 ;1} \right)\)

\( \Rightarrow \overrightarrow u .\;\,\overrightarrow v  = 0.\sqrt 3  + \left( { - 5} \right).1 =  - 5.\)

HĐ4

Cho ba vectơ \(\overrightarrow u  = ({x_1};{y_1}),\;\overrightarrow v  = ({x_2};{y_2}),\;\overrightarrow w  = ({x_3};{y_3}).\)

a) Tính \(\overrightarrow u .\left( {\overrightarrow v  + \overrightarrow w } \right),\;\overrightarrow u .\overrightarrow v  + \overrightarrow u .\overrightarrow w \) theo tọa độ của các vectơ \(\overrightarrow u ,\overrightarrow v ,\overrightarrow w .\)

b) So sánh \(\overrightarrow u .\left( {\overrightarrow v  + \overrightarrow w } \right)\) và \(\;\overrightarrow u .\overrightarrow v  + \overrightarrow u .\overrightarrow w \)

c) So sánh \(\;\overrightarrow u .\overrightarrow v \) và \(\overrightarrow v .\overrightarrow u \)

Phương pháp giải:

Cho \(\overrightarrow u  = \left( {x;y} \right)\) và \(\overrightarrow v  = \left( {x';y'} \right)\), khi đó: \(\overrightarrow u .\overrightarrow v  = x.x' + y.y'\)

Lời giải chi tiết:

a) Ta có: \(\overrightarrow u  = ({x_1};{y_1}),\;\overrightarrow v  = ({x_2};{y_2}),\;\overrightarrow w  = ({x_3};{y_3}).\)

\(\begin{array}{l} \Rightarrow \overrightarrow v  + \overrightarrow w  = ({x_2};{y_2}) + ({x_3};{y_3}) = \left( {{x_2} + {x_3};{y_2} + {y_3}} \right)\\ \Rightarrow \overrightarrow u .\left( {\overrightarrow v  + \overrightarrow w } \right) = {x_1}.\left( {{x_2} + {x_3}} \right) + {y_1}.\left( {{y_2} + {y_3}} \right)\end{array}\)

Và: \(\;\overrightarrow u .\overrightarrow v  + \overrightarrow u .\overrightarrow w  = \left( {{x_1}.{x_2} + {y_1}.{y_2}} \right) + \left( {{x_1}.{x_3} + {y_1}.{y_3}} \right)\)\( = {x_1}.{x_2} + {y_1}.{y_2} + {x_1}.{x_3} + {y_1}.{y_3}.\)

b) Vì \({x_1}.{x_2} + {y_1}.{y_2} + {x_1}.{x_3} + {y_1}.{y_3}\)\( = \left( {{x_1}.{x_2} + {x_1}.{x_3}} \right) + \left( {{y_1}.{y_2} + {y_1}.{y_3}} \right)\)\( = {x_1}.\left( {{x_2} + {x_3}} \right) + {y_1}.\left( {{y_2} + {y_3}} \right)\)

Nên \(\overrightarrow u .\left( {\overrightarrow v  + \overrightarrow w } \right) = \;\overrightarrow u .\overrightarrow v  + \overrightarrow u .\overrightarrow w \)

c) Ta có: \(\overrightarrow u  = ({x_1};{y_1}),\;\overrightarrow v  = ({x_2};{y_2})\)

\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow u .\overrightarrow v  = {x_1}.{x_2} + {y_1}.{y_2}\\\overrightarrow v .\overrightarrow u  = {x_2}.{x_1} + {y_2}.{y_1}\end{array} \right.\)\( \Leftrightarrow \;\overrightarrow u .\overrightarrow v  = \overrightarrow v .\overrightarrow u \)

Luyện tập 4

Cho tam giác ABC với A(-1; 2), B(8; -1), C(8; 8). Gọi H là trực tâm của tam giác.

a) Chứng minh rằng \(\overrightarrow {AH} .\overrightarrow {BC}  = \overrightarrow 0 \) và \(\overrightarrow {BH} .\overrightarrow {CA}  = \overrightarrow 0 \)

b) Tìm tọa độ của H.

c) Giải tam giác ABC.

Phương pháp giải:

a)  \(\overrightarrow u  \bot \overrightarrow v  \Leftrightarrow \overrightarrow u .\overrightarrow v  = 0\)

b) Lập hệ PT biết \(\overrightarrow {AH} .\overrightarrow {BC}  = \overrightarrow 0 \) và \(\overrightarrow {BH} .\overrightarrow {CA}  = \overrightarrow 0 \).

c) Nếu vectơ \(\overrightarrow {AB} (x;y) \) thì \(\left| {\overrightarrow {AB} } \right| = \sqrt {{x^2} + {y^2}} \)

Lời giải chi tiết:

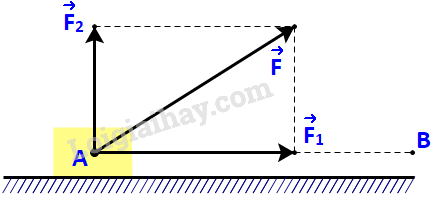
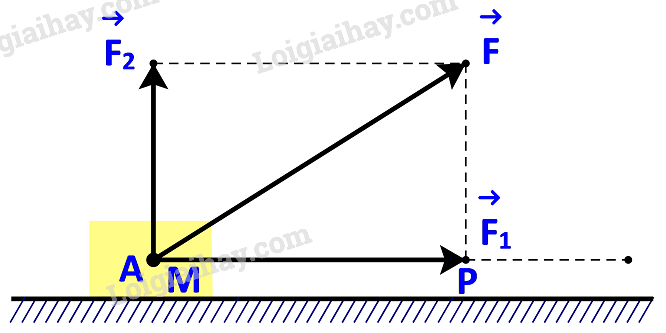
a) \( AH \bot BC\) và \(BH \bot CA\)

\( \Rightarrow \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = {90^o} \Leftrightarrow \cos \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = 0\) . Do đó \(\overrightarrow {AH} .\overrightarrow {BC}  = \overrightarrow 0 \)

Tương tự suy ra \(\overrightarrow {BH} .\overrightarrow {CA}  = \overrightarrow 0 \).

b) Gọi H có tọa độ (x; y)

\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH}  = (x - ( - 1);y - 2) = (x + 1;y - 2)\\\overrightarrow {BH}  = (x - 8;y - ( - 1)) = (x - 8;y + 1)\end{array} \right.\)

Ta có: \(\overrightarrow {AH} .\overrightarrow {BC}  = \overrightarrow 0 \) và \(\overrightarrow {BC}  = (8 - 8;8 - ( - 1)) = (0;9)\)

\((x + 1).0 + (y - 2).9 = 0 \Leftrightarrow 9.(y - 2) = 0 \Leftrightarrow y = 2.\)

Lại có: \(\overrightarrow {BH} .\overrightarrow {CA}  = \overrightarrow 0 \) và \(\overrightarrow {CA}  = ( - 1 - 8;2 - 8) = ( - 9; - 6)\)

\(\begin{array}{l}(x - 8).( - 9) + (y + 1).( - 6) = 0\\ \Leftrightarrow  - 9x + 72 + 3.( - 6) = 0\\ \Leftrightarrow  - 9x + 54 = 0\\ \Leftrightarrow x = 6.\end{array}\)

Vậy H có tọa độ (6; 2)

c) Ta có: \(\overrightarrow {AB}  = (8 - ( - 1); - 1 - 2) = (9; - 3)\)\( \Rightarrow AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{9^2} + {{( - 3)}^2}}  = 3\sqrt {10} \)

Và  \(\overrightarrow {BC}  = (0;9) \Rightarrow BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{0^2} + {9^2}}  = 9\);

\(\overrightarrow {CA}  = ( - 9; - 6)\)\( \Rightarrow AC = \left| {\overrightarrow {CA} } \right| = \sqrt {{{( - 9)}^2} + {{( - 6)}^2}}  = 3\sqrt {13} .\)

Áp dụng định lí cosin cho tam giác ABC, ta có:

\(\cos \widehat A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{{\left( {3\sqrt {13} } \right)}^2} + {{\left( {3\sqrt {10} } \right)}^2} - {{\left( 9 \right)}^2}}}{{2.3\sqrt {13} .3\sqrt {10} }} \approx 0,614\)\( \Rightarrow \widehat A \approx 52,{125^o}\)

\(\cos \widehat B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{{\left( 9 \right)}^2} + {{\left( {3\sqrt {10} } \right)}^2} - {{\left( {3\sqrt {13} } \right)}^2}}}{{2.9.3\sqrt {10} }} = \frac{{\sqrt {10} }}{{10}}\)\( \Rightarrow \widehat B \approx 71,{565^o}\)

\( \Rightarrow \widehat C \approx 56,{31^o}\)

Vậy tam giác ABC có: \(a = 9;b = 3\sqrt {13} ;c = 3\sqrt {10} \); \(\widehat A \approx 52,{125^o};\widehat B \approx 71,{565^o};\widehat C \approx 56,{31^o}.\)

Vận dụng

Một lực \(\overrightarrow F \) không đổi tác động vào một vật và điểm đặt của lực chuyển động thẳng từ A đến B. Lực \(\overrightarrow F \) được phân tích thành hai lực thành phần là \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) \((\overrightarrow F  = \overrightarrow {{F_1}}  + \overrightarrow {{F_2}} \;).\)

a) Dựa vào tính chất của tích vô hướng, hãy giải thích vì sao công sinh bởi lực \(\overrightarrow F \) (đã được đề cập ở trên) bằng tổng của các công sinh bởi các lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).

b) Giả sử các lực thành phần \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \)tương ứng cùng phương, vuông góc với phương chuyển động của vật. Hãy tìm mối quan hệ giữa các công sinh bởi lực \(\overrightarrow F \) và lực \(\overrightarrow {{F_1}} \).

Phương pháp giải:

Khi lực \(\overrightarrow F \) không đổi tác dụng lên một vật và điểm đặt chuyển dời một đoạn s theo hướng hợp với hướng của lực góc α thì công sinh bởi lực đó là: \(A = F.{\rm{ }}s.\cos \alpha \)

Lời giải chi tiết:

a)

Gọi \(A,{A_1},{A_2}\) lần lượt là công sinh bởi lực \(\overrightarrow F \), \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).

Ta cần chứng minh: \(A = {A_1} + {A_2}\)

Xét lực \(\overrightarrow F \), công sinh bởi lực \(\overrightarrow F \) là: \(A = \left| {\overrightarrow F } \right|.{\rm{ AB}}.\cos \left( {\overrightarrow F ,\overrightarrow {AB} } \right) = \overrightarrow F .\overrightarrow {AB} \)

Tương tự, ta có: \({A_1} = \overrightarrow {{F_1}} .\overrightarrow {AB} \), \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB} \)

Áp dụng tính chất của tích vô hướng ta có:

\({A_1} + {A_2} = \overrightarrow {{F_1}} .\overrightarrow {AB}  + \overrightarrow {{F_2}} .\overrightarrow {AB}  = \left( {\overrightarrow {{F_1}}  + \overrightarrow {{F_2}} } \right).\overrightarrow {AB}  = \overrightarrow F .\overrightarrow {AB}  = A\)

b)

Vì \(\overrightarrow {{F_2}} \)tương ứng vuông góc với phương chuyển động nên \(\overrightarrow {{F_2}}  \bot \overrightarrow {AB} \)

Do đó: công sinh bởi lực \(\overrightarrow {{F_2}} \) là: \({A_2} = \overrightarrow {{F_2}} .\overrightarrow {AB}  = 0\)

Mà \(A = {A_1} + {A_2}\)

\( \Rightarrow A = {A_1}\)

Vậy công sinh bởi lực \(\overrightarrow F \) bằng công sinh bởi lực \(\overrightarrow {{F_1}} \).