Giải mục II trang 61, 62, 63 SGK Toán 10 tập 2 - Cánh diềuCho điểm M trong mặt phẳng toạ độ Oxy. a) Vē vecto OM b) Nêu cách xác định toạ độ của điểm M. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
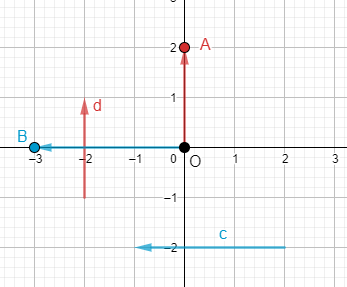
Hoạt động 2 Cho điểm M trong mặt phẳng toạ độ Oxy. a) Vē vecto \(\overrightarrow {OM} \). b) Nêu cách xác định toạ độ của điểm M. Lời giải chi tiết: a) Ta có vecto \(\overrightarrow {OM}\) với điểm đầu là O và điểm cuối là M như hình 4. b) Cách xác định tọa độ điểm M là: • Từ M kẻ đường thẳng vuông góc với trục hoành và cắt trục hoành tại điểm H ứng với số a. Số a là hoành độ của điểm M. • Từ M kẻ đường thẳng vuông góc với trục tung và cắt trục tung tại điểm K ứng với số b. Số b là tung độ của điểm M. Cặp số (a; b) là toạ độ của điểm M trong mặt phẳng toạ độ Oxy. Hoạt động 3 Trong mặt phẳng toạ độ Oxy, cho vectơ \(\overrightarrow u \) (Hình 7). Hãy xác định điểm A sao cho \(\overrightarrow {OA} = \overrightarrow u \). Lời giải chi tiết: Để xác định điểm A, ta làm như sau (Hình 8): • Qua O kẻ đường thẳng d song song với giá của vectơ \(\overrightarrow u \). • Lấy điểm A trên đường thẳng d sao cho hai vectơ \(\overrightarrow {OA} \), \(\overrightarrow u \) cùng hướng và độ dài đoạn thẳng OA bằng độ dài vectơ \(\overrightarrow u \). Luyện tập – vận dụng 1 Tìm tọa độ của các vecto \(\overrightarrow c ,\overrightarrow d \) trong Hình 11.
Lời giải chi tiết:
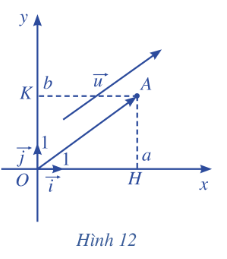
Ta vẽ vecto \(\overrightarrow {OA} = \overrightarrow d \) và \(A\left( {0;2} \right)\). Tọa độ \(\overrightarrow {OA} \) chính là tọa độ của điểm A nên \(\overrightarrow d = \left( {2;2} \right)\). Ta vẽ vecto \(\overrightarrow {OB} = \overrightarrow c \) và \(A\left( { - 3;0} \right)\). Tọa độ \(\overrightarrow {OB} \) chính là tọa độ của điểm B nên \(\overrightarrow c = \left( { - 3;0} \right)\). Hoạt động 4 Trong mặt phẳng toạ độ Oxy, cho vectơ\(\overrightarrow u {\rm{ }} = {\rm{ }}\left( {a;{\rm{ }}b} \right)\) . Ta chọn điểm A sao cho\(\overrightarrow {OA} {\rm{ }} = {\rm{ }}\overrightarrow u \) . Xét vectơ đơn vị \(\overrightarrow i \) trên trục hoành Ox và vectơ đơn vị \(\overrightarrow j \) ở trên trục tung Oy (Hình 12). a) Tìm hoành độ và tung độ của điểm A. b) Biểu diễn vectơ OH qua vectơ \(\overrightarrow i \). c) Biểu diễn vectơ OK qua vecto \(\overrightarrow j \). d) Chứng tỏ rằng\(\overrightarrow u = a\overrightarrow i + b\overrightarrow j \).
Lời giải chi tiết: a) Do \(\overrightarrow {OA} = \overrightarrow u \) nên tọa độ vecto \(\overrightarrow {OA} = \left( {a;b} \right)\). Vậy tọa độ điểm A là: \(A\left( {a;b} \right)\). b) Tọa độ điểm H là \(H\left( {a;0} \right)\) nên \(\overrightarrow {OH} = \left( {a;0} \right)\). Do đó, \(\overrightarrow {OH} = a\overrightarrow i \). c) Tọa độ điểm K là \(K\left( {0;b} \right)\) nên \(\overrightarrow {OK} = \left( {0;b} \right)\). Do đó, \(\overrightarrow {OK} = b\overrightarrow j \). d) Ta có: \(\overrightarrow u = \overrightarrow {OA} = \overrightarrow {OH} + \overrightarrow {OK} = a\overrightarrow i + b\overrightarrow j \) (ĐPCM). Luyện tập – vận dụng 2 Trong mặt phẳng tọa độ Oxy, cho điểm B(-1; 0) và vecto \(\overrightarrow v = \left( {0; - 7} \right)\). a) Biểu diễn vecto \(\overrightarrow v \) qua hai vecto \(\overrightarrow i ,\overrightarrow j \). b) Biểu diễn vecto \(\overrightarrow {OB} \) qua hai vecto\(\overrightarrow i ,\overrightarrow j \). Lời giải chi tiết: a) Vì \(\overrightarrow v = \left( {0; - 7} \right)\) nên \(\overrightarrow v = 0\overrightarrow i + \left( { - 7} \right)\overrightarrow j = - 7\overrightarrow j \). b) Vì B có tọa độ là (-1; 0) nên \(\overrightarrow {OB} = \left( { - 1;{\rm{ }}0} \right)\). Do đó: \(\overrightarrow {OB} = \left( { - 1} \right)\overrightarrow i + 0\overrightarrow j = - \overrightarrow i \).
|





















Danh sách bình luận