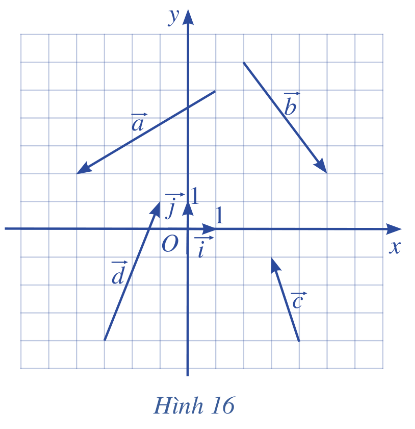
Giải bài 1 trang 65 SGK Toán 10 tập 2 – Cánh diềuTìm tọa độ của các vecto trong Hình 16 và biểu diễn mỗi vecto đó qua hai vecto Quảng cáo
Đề bài Tìm tọa độ của các vecto trong Hình 16 và biểu diễn mỗi vecto đó qua hai vecto \(\overrightarrow i , \overrightarrow j \).
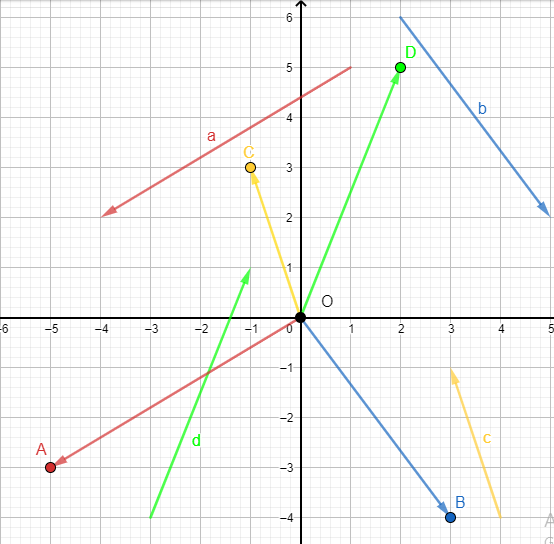
Phương pháp giải - Xem chi tiết Vẽ các vecto \(\overrightarrow {OA} = \overrightarrow a \), \(\overrightarrow {OB} = \overrightarrow b \), \(\overrightarrow {OC} = \overrightarrow c \), \(\overrightarrow {OD} = \overrightarrow d \). Tọa độ của 4 điểm A, B, C, D là tọa độ của 4 vecto. Để biểu diễn các vecto qua vecto đơn vị: \(\overrightarrow u {\rm{ }} = {\rm{ }}\left( {a;{\rm{ }}b} \right) \Leftrightarrow \overrightarrow u = a\overrightarrow i + b\overrightarrow j \). Lời giải chi tiết a) Vẽ các vecto \(\overrightarrow {OA} = \overrightarrow a \), \(\overrightarrow {OB} = \overrightarrow b \), \(\overrightarrow {OC} = \overrightarrow c \), \(\overrightarrow {OD} = \overrightarrow d \).
Dựa vào hình vẽ, ta thấy tọa độ của 4 điểm A, B, C, D là: \(A\left( { - 5; - 3} \right)\), \(B\left( {3; - 4} \right)\), \(C\left( { - 1;3} \right)\), \(D\left( {2;5} \right)\). Do đó \(\overrightarrow a = \overrightarrow {OA} = \left( { - 5; - 3} \right)\), \(\overrightarrow b = \overrightarrow {OB} = \left( {3; - 4} \right)\), \(\overrightarrow c = \overrightarrow {OC} = \left( { - 1;3} \right)\), \(\overrightarrow d = \overrightarrow {OD} = \left( {2;5} \right)\). b) Vì \(\overrightarrow a = \overrightarrow {OA} = \left( { - 5; - 3} \right)\) nên \(\overrightarrow a = \left( { - 5} \right)\overrightarrow i + \left( { - 3} \right)\overrightarrow j = - 5\overrightarrow i - 3\overrightarrow j \). Vì \(\overrightarrow b = \overrightarrow {OB} = \left( {3; - 4} \right)\) nên \(\overrightarrow b = 3\overrightarrow i + \left( { - 4} \right)\overrightarrow j = 3\overrightarrow i - 4\overrightarrow j \). Vì \(\overrightarrow c = \overrightarrow {OC} = \left( { - 1;3} \right)\) nên \(\overrightarrow c = \left( { - 1} \right)\overrightarrow i + \left( 3 \right)\overrightarrow j = - \overrightarrow i + 3\overrightarrow j \). Vì \(\overrightarrow d = \overrightarrow {OD} = \left( {2;5} \right)\) nên \(\overrightarrow d = 2\overrightarrow i + 5\overrightarrow j \).
|




















Danh sách bình luận