Giải mục 1 trang 46, 47 SGK Toán 7 tập 1 - Kết nối tri thức

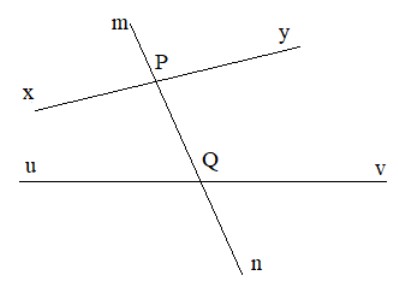
Câu hỏi 1

Cho đường thẳng mn cắt đường thẳng xy và uv lần lượt tại hai điểm P và Q (H.3.17).Em hãy kể tên:

a) Hai cặp góc so le trong

b) Bốn cặp góc đồng vị.

Phương pháp giải:

Vẽ hình, nhận diện các cặp góc so le trong, đồng vị.

Lời giải chi tiết:

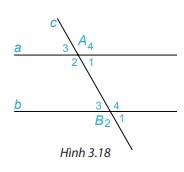
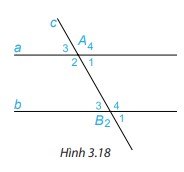
a) Hai cặp góc so le trong là: góc xPn và góc mQv; góc yPn và góc uQm

b) Bốn cặp góc đồng vị là: góc mPy và góc mQv; góc yPn và góc vQn; góc mPx và góc mQu; góc xPn và góc uQn.

HĐ 1

Trên Hình 3.18, cho biết hai góc so le trong A₁ và B₃ bằng nhau và bằng \(60^\circ \).

Hãy tính và so sánh hai góc so le trong còn lại A₂ và B₄.

Phương pháp giải:

Sử dụng tính chất 2 góc kề bù: Tổng 2 góc kề bù bằng 180 độ

Lời giải chi tiết:

+) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)

\(\begin{array}{l} \Rightarrow 60^\circ  + \widehat {{A_2}} = 180^\circ \\ \Rightarrow \widehat {{A_2}} = 180^\circ  - 60^\circ  = 120^\circ \end{array}\)

+) Vì \(\widehat {{B_3}} + \widehat {{B_4}} = 180^\circ \) (2 góc kề bù)

\(\begin{array}{l} \Rightarrow 60^\circ  + \widehat {{B_4}} = 180^\circ \\ \Rightarrow \widehat {{B_4}} = 180^\circ  - 60^\circ  = 120^\circ \end{array}\)

Vậy hai góc so le trong còn lại A₂ và B₄ bằng nhau và bằng \(120^\circ \).

HĐ 2

Trên Hình 3.18, cho biết hai góc so le trong A₁ và B₃ bằng nhau và bằng \(60^\circ \).

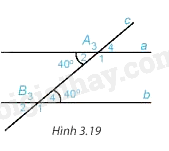
Chọn hai góc đồng vị rồi tính và so sánh hai góc đó.

Phương pháp giải:

Sử dụng tính chất: Tổng 2 góc kề bù bằng 180 độ hoặc 2 góc đối đỉnh thì bằng nhau

Lời giải chi tiết:

Chọn cặp góc đồng vị: góc A₁ và góc B₁

Ta có: \(\widehat {{A_1}} = 60^\circ ;\widehat {{B_3}} = 60^\circ \)

\(\widehat {{B_1}} = \widehat {{B_3}}\) (2 góc đối đỉnh)

\( \Rightarrow \widehat {{B_1}} = 60^\circ \)

Vậy hai góc A₁ và góc B₁ đồng vị bằng nhau và bằng \(60^0\)

Luyện tập 1

a) Cho hình 3.19, biết \(\widehat {{A_2}} = 40^\circ ;\widehat {{B_4}} = 40^\circ \). Em hãy cho biết số đo các góc còn lại.

b) Các cặp góc A₁ và B₄; A₂ và B₃ được gọi là các cặp góc trong cùng phía. Tính tổng: \(\widehat {{A_1}} + \widehat {{B_4}};\widehat {{A_2}} + \widehat {{B_3}}\).

Phương pháp giải:

Sử dụng tính chất: Tổng 2 góc kề bù bằng 180 độ hoặc 2 góc đối đỉnh thì bằng nhau

Đường thẳng c cắt 2 đường thẳng, tạo thành 1 cặp góc so le trong bằng nhau.

Lời giải chi tiết:

a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (2 góc kề bù)

\( \Rightarrow \widehat {{A_1}} + 40^\circ  = 180^\circ \)

\( \Rightarrow \widehat {{A_1}} = 180^\circ  - 40^\circ  = 140^\circ \)

Ta có: \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 140^\circ \) nên \(\widehat {{A_3}} = 140^\circ \)

\(\widehat {{A_2}} = \widehat {{A_4}}\)(2 góc đối đỉnh), mà \(\widehat {{A_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)

Vì \(\widehat {{A_2}} = \widehat {{B_4}} = 40^\circ \), mà 2 góc này ở vị trí so le trong

\( \Rightarrow \) 2 góc đồng vị bằng nhau nên

 \(\begin{array}{l}\widehat {{A_1}} = \widehat {{B_1}} = 140^\circ ;\widehat {{A_2}} = \widehat {{B_2}} = 40^\circ ;\\\widehat {{A_3}} = \widehat {{B_3}} = 140^\circ ;\widehat {{A_4}} = \widehat {{B_4}} = 40^\circ \end{array}\)

b) Ta có:

\(\begin{array}{l}\widehat {{A_1}} + \widehat {{B_4}} = 140^\circ  + 40^\circ  = 180^\circ \\\widehat {{A_2}} + \widehat {{B_3}} = 40^\circ  + 140^\circ  = 180^\circ \end{array}\)