Giải mục 2 trang 47, 48, 49 SGK Toán 7 tập 1 - Kết nối tri thức1. Quan sát Hình 3.22 và giải thích vì sao AB // CD. 2. Tìm trên Hình 3.23 hai đường thẳng song song với nhau và giải thích vì sao chúng song song? Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
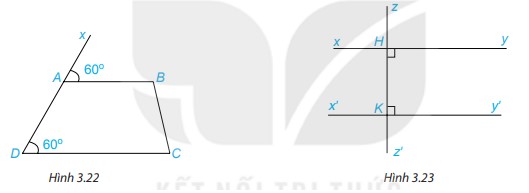
Luyện tập 2 1. Quan sát Hình 3.22 và giải thích vì sao AB // CD. 2. Tìm trên Hình 3.23 hai đường thẳng song song với nhau và giải thích vì sao chúng song song?
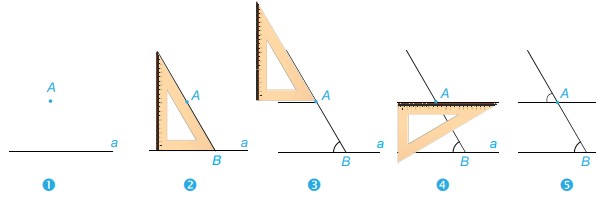
Phương pháp giải: Đường thẳng c cắt hai đường thẳng phân biệt, tạo thành một cặp góc so le trong hoặc cặp góc đồng vị bằng nhau thì 2 đường thẳng đó song song Lời giải chi tiết: 1. Vì \(\widehat {BAx} = \widehat {CDA} ( = 60^\circ )\) Mà 2 góc này ở vị trí đồng vị nên AB//CD (Dấu hiệu nhận biết hai đường thẳng song song) 2. Ta có: \(\widehat {zKy'} + \widehat {y'Kz'} = 180^\circ \) (2 góc kề bù) \(\begin{array}{l} 90^\circ + \widehat {y'Kz'} = 180^\circ \\ \text{suy ra } \widehat {y'Kz'} = 180^\circ - 90^\circ = 90^\circ \end{array}\) Vì \(\widehat {yHz'} = \widehat {y'Kz'}\) Mà 2 góc này ở vị trí đồng vị nên xy // x’y’ (Dấu hiệu nhận biết hai đường thẳng song song) Chú ý: 2 đường thẳng cùng vuông góc với 1 đường thẳng thứ ba thì 2 đường thẳng đó song song. Thực hành 1 Cho đường thẳng a và điểm A nằm ngoài đường thẳng a. Để vẽ đường thẳng b đi qua A và song song với a, ta có thể sử dụng góc nhọn \(60^\circ \) của êke để vẽ như sau:
Tại sao khi vẽ như trên ta lại khẳng định được hai đường thẳng a và b song song với nhau. Phương pháp giải: Sử dụng dấu hiệu nhận biết 2 đường thẳng song song Lời giải chi tiết: Ta thấy, khi vẽ hình như trên, ta đã vẽ 2 góc A và B có số đo bằng nhau (đều bằng \(60^\circ \)). Mà 2 góc này ở vị trí đồng vị Vậy a//b (Dấu hiệu nhận biết 2 đường thẳng song song) Thực hành 2 Dùng góc vuông hay góc 30\(^\circ \)của êke (thay cho góc 60\(^\circ \)) để vẽ đường thẳng đi qua và song song với đường thẳng a cho trước. Phương pháp giải: Đặt góc vuông hay góc 30\(^\circ \) của êke thay cho góc 60\(^\circ \) trong Thực hành 1 Lời giải chi tiết: + Dùng góc vuông: Bước 1: Vẽ đường thẳng a , điểm A nằm ngoài đường thẳng a
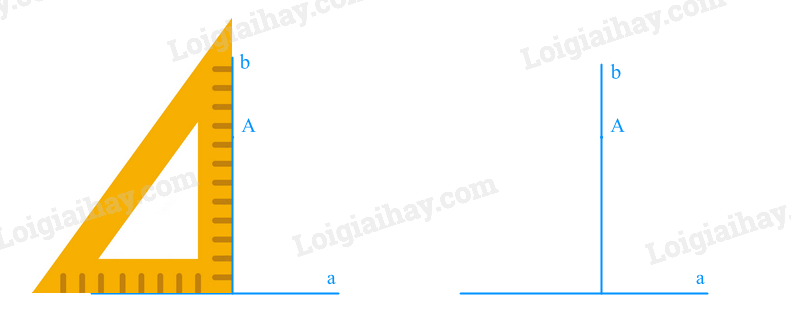
Bước 2: Đặt ê ke sao cho 1 cạnh của góc vuông của ê ke nằm trên đường thẳng a, 1 cạnh góc vuông còn lại đi qua điểm A, ta kẻ đường thẳng b đi qua A, vuông góc với a.
Bước 3: Kẻ đường thẳng đi qua A, vuông góc với đường thẳng b. Ta được đường thẳng b' đi qua A và song song với a.
+ Dùng góc 30\(^\circ \)của êke: Bước 1: Vẽ đường thẳng a , điểm A nằm ngoài đường thẳng a
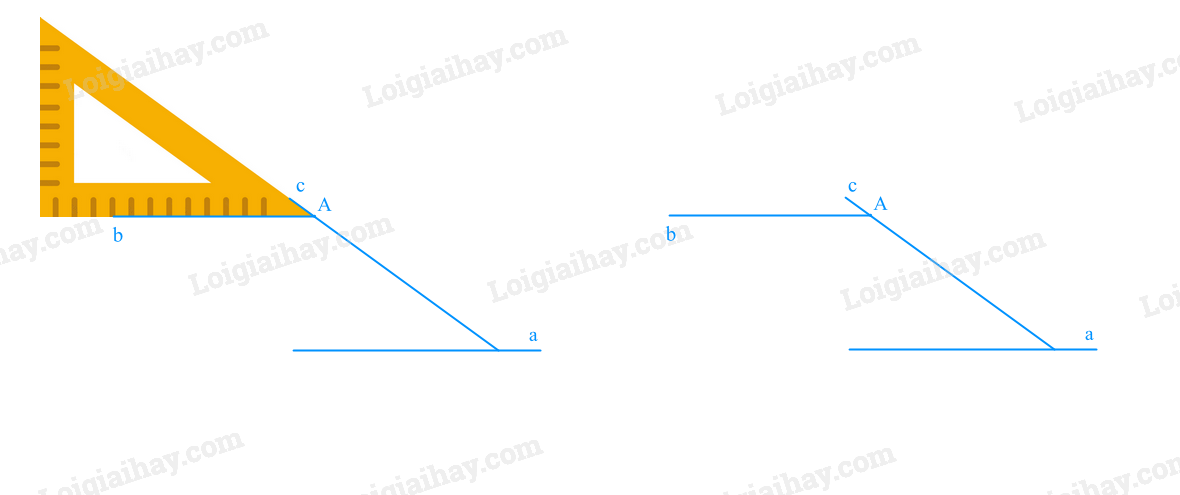
Bước 2: Đặt ê ke sao cho góc nhọn 30\(^\circ \) và 1 cạnh của góc vuông của ê ke nằm trên đường thẳng a, cạnh đối diện với góc vuông đi qua điểm A, ta kẻ đường thẳng c đi qua cạnh đối diện với góc vuông của ê ke.
Bước 3: Dịch chuyển ê ke theo đường thẳng c cho đến khi điểm A trùng với đỉnh của góc nhọn 30\(^\circ \).
Bước 4: Kẻ đường thẳng b đi qua A và 1 cạnh của góc 30\(^\circ \)
Ta được đường thẳng b đi qua A và song song với a.
|

























Danh sách bình luận