Giải tuần 28: Giới thiệu tỉ số. Tìm hai số khi biết tổng và tỉ số của hai số đó. Luyện tập chung trang 36

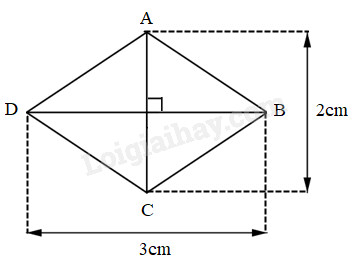
Bài 1

Khoanh vào chữ đặt trước kết quả đúng:

Diện tích của hình thoi ABCD là:

A. \(4cm^2\)                    B. \(6cm^2\)                  C. \(3cm^2\)                  D. \(9cm^2\)

Phương pháp giải:

Diện tích hình thoi bằng tích của độ dài hai đường chéo chia cho \(2\) (cùng một đơn vi đo).

Lời giải chi tiết:

Diện tích của hình thoi ABCD là:

\(\dfrac{3\times 2}{2} = 3\;(cm^2)\)

                  Đáp số : \(3cm^2\)

Chọn đáp án C. 

Bài 2

Viết vào ô trống cho thích hợp (theo mẫu):

Phương pháp giải:

Tỉ số của \(a\) và \(b\) là \(a:b\) hay \(\dfrac{a}{b}\) (\(b\) khác \(0\)).

Lời giải chi tiết:

Bài 3

Viết tiếp vào chỗ chấm:

Câu lạc bộ cờ vua có \(13\) bạn nam và \(15\) bạn nữ.

a) Tỉ số của số bạn nam và số bạn nữ trong câu lạc bộ cờ vua là: ……..

b) Tỉ số của số bạn nam và số bạn của câu lạc bộ cờ vua là: ……..

c) Tỉ số của số bạn nữ và số bạn của câu lạc bộ cờ vua là: ……..

Phương pháp giải:

Tỉ số của \(a\) và \(b\) là \(a:b\) hay \(\dfrac{a}{b}\) (\(b\) khác \(0\)).

Lời giải chi tiết:

a) Tỉ số của số bạn nam và số bạn nữ trong câu lạc bộ cờ vua là: \(\dfrac{13}{15}\).

b) Câu lạc bộ cờ vua có tất cả số bạn là: \(13 + 15 = 28\) (bạn)

    Tỉ số của số bạn nam và số bạn của câu lạc bộ cờ vua là: \(\dfrac{13}{{28}}\).

c) Tỉ số của số bạn nữ và số bạn của câu lạc bộ cờ vua là: \(\dfrac{15}{{28}}\).

Bài 4

Viết tỉ số thích hợp vào chỗ chấm:

a) Trong nhóm học sinh biết bơi, số học sinh nam gấp đôi số học sinh nữ. Tỉ số giữa số học sinh nữ và số học sinh nam trong nhóm học sinh đó là ……

b) Có hai đoạn dây, đoạn dây thứ nhất dài gấp 3 lần đoạn dây thứ hai. Tỉ số giữa đoạn dây thứ nhất và đoạn dây thứ hai là ……

c) Trong vườn, số gà mái bằng số gà trống. Tỉ số giữa số gà trống và số gà mái là ……

d) Số bông hoa lan bằng nửa số bông hoa huệ. Tỉ số giữa số bông lan và số bông huệ là ……

Phương pháp giải:

Tỉ số của \(a\) và \(b\) là \(a:b\) hay \(\dfrac{a}{b}\) (\(b\) khác \(0\)).

Lời giải chi tiết:

Viết tỉ số thích hợp vào chỗ chấm:

a) Trong nhóm học sinh biết bơi, số học sinh nam gấp đôi số học sinh nữ. Tỉ số giữa số học sinh nữ và số học sinh nam trong nhóm học sinh đó là \(1:2\) hay \(\dfrac{1}{2}\).

b) Có hai đoạn dây, đoạn dây thứ nhất dài gấp 3 lần đoạn dây thứ hai. Tỉ số giữa đoạn dây thứ nhất và đoạn dây thứ hai là \(3:1\) hay \(\dfrac{3}{1}\).

c) Trong vườn, số gà mái bằng số gà trống. Tỉ số giữa số gà trống và số gà mái là \(1:1\) hay \(\dfrac{1}{1}\).

d) Số bông hoa lan bằng nửa số bông hoa huệ. Tỉ số giữa số bông lan và số bông huệ là \(1:2\) hay \(\dfrac{1}{2}\).

Bài 5

Viết số hoặc tỉ số thích hợp vào chỗ chấm:

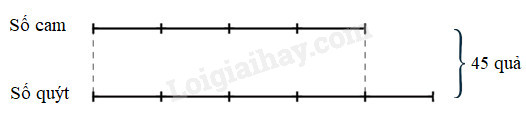
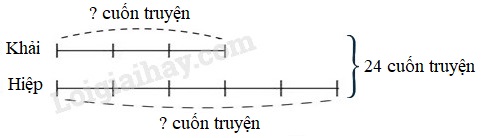
Biểu thị số cam là …….. phần bằng nhau.

Biểu thị số quýt là …….. phần như thế.

Tỉ số của số cam và số quýt là ……..

Tổng số phần bằng nhau là …….. phần

Tổng số cam và quýt là …….. quả

Số cam là: ……..

Số quýt là: ……..

Phương pháp giải:

Quan sát kĩ sơ đồ để hoàn thành bài toán đã cho.

Lời giải chi tiết:

Biểu thị số cam là 4 phần bằng nhau.

Biểu thị số quýt là 5 phần như thế.

Tỉ số của số cam và số quýt là \(\dfrac{4}{5}\).

Tổng số phần bằng nhau là 9 phần. 

Tổng số cam và quýt là 45 quả.

Số cam là: 45 : 9 × 4 = 20 quả.

Số quýt là: 45 – 20 = 25 quả. 

Bài 6

Khải và Hiệp có 24 cuốn truyện. Số truyện của Khải bằng \(\dfrac{3}{5}\) số truyện của Hiệp. Hỏi mỗi bạn có bao nhiêu cuốn truyện?

Phương pháp giải:

1. Vẽ sơ đồ

2. Tìm tổng số phần bằng nhau.

3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.

4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).

5. Tìm số lớn (lấy tổng hai số trừ đi số bé, …).

Lời giải chi tiết:

Ta có sơ đồ:

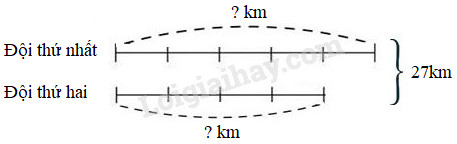
Theo sơ đồ, tổng số phần bằng nhau là:

 3 + 5 = 8 (phần)

Khải có số cuốn truyện là:

24 : 8 × 3 = 9 (cuốn truyện)

Hiệp có số cuốn truyện là:

24 – 9 = 15 (cuốn truyện)

Đáp số: Khải: 9 cuốn truyện;

               Hiệp: 15 cuốn truyện.

Bài 7

Hai đội thi công được 27km đường. Đội thứ nhất sửa được đoạn đường bằng \(\dfrac{5}{4}\) đoạn đường đội thứ hai sửa được. Hỏi mỗi đội sửa được bao nhiêu ki-lô-mét đường?

Phương pháp giải:

1. Vẽ sơ đồ

2. Tìm tổng số phần bằng nhau.

3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.

4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).

5. Tìm số lớn (lấy tổng hai số trừ đi số bé, …).

Lời giải chi tiết:

Ta có sơ đồ:

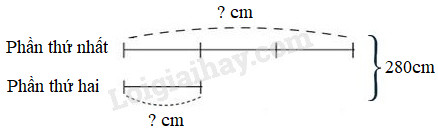
Theo sơ đồ, tổng số phần bằng nhau là:

5 + 4 = 9 (phần)

Đội thứ nhất sửa được số ki-lô-mét đường là:

27 : 9 × 5 = 15 (km)

Đội thứ hai sửa được số ki-lô-mét đường là:

27 – 15 = 12 (km)

Đáp số: Đội thứ nhất: 15km;

            Đội thứ hai: 12km.

Bài 8

Một tấm gỗ dài 280cm, người ta cắt thành hai phần, phần thứ nhất dài gấp 3 lần phần thứ hai. Hỏi mỗi phần dài bao nhiêu xăng-ti-mét?

Phương pháp giải:

1. Vẽ sơ đồ

2. Tìm tổng số phần bằng nhau.

3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.

4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).

5. Tìm số lớn (lấy tổng  hai số trừ đi số bé, …).

Lời giải chi tiết:

Ta có sơ đồ:

Theo sơ đồ, tổng số phần bằng nhau là:

3 + 1 = 4 (phần)

Phần thứ nhất dài số xăng-ti-mét là:

280 : 4 × 3 = 210 (cm)

Phần thứ hai dài số xăng-ti-mét là:

280 – 210 = 70 (cm)

Đáp số: Phần thứ nhất: 210cm;

             Phần thứ hai: 70cm.

Vui học

Viết tiếp vào chỗ chấm để được câu trả lời đúng:

Tại một cửa hàng bày bán các giỏ hoa quả, chủ cửa hàng cho biết mỗi giỏ hoa quả nặng 2kg, trong đó có một phần là nho, 3 phần là các loại hoa quả khác. Hỏi trong mỗi giỏ có bao nhiêu gam nho và bao nhiêu gam hoa quả khác? 

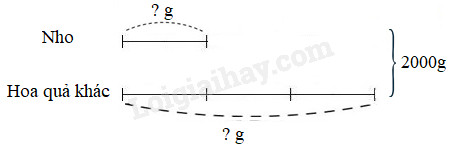
Phương pháp giải:

1. Vẽ sơ đồ

2. Tìm tổng số phần bằng nhau.

3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.

4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).

5. Tìm số lớn (lấy tổng hai số trừ đi số bé, …).

Lời giải chi tiết:

Đổi : 2kg = 2000g.

Ta có sơ đồ:

Theo sơ đồ, tổng số phần bằng nhau là:

1 + 3 = 4 (phần)

Trong mỗi giỏ có số gam nho là:

2000 : 4 × 1 = 500 (g)

Trong mỗi giỏ có số gam hoa quả khác là:

2000 – 500 = 1500 (g)

                       Đáp số: Nho: 500g;

                              Hoa quả khác: 1500g.