Giải tuần 27: Luyện tập chung. Hình thoi. Diện tích hình thoi trang 33

Bài 1

Rút gọn phân số: 

a) \(\dfrac{6}{{10}} =  \ldots \)                           \(\dfrac{{96}}{{72}} =  \ldots \)

b) \(\dfrac{{60}}{{90}} =  \ldots \)                           \(\dfrac{{35}}{{25}} =  \ldots \)

Phương pháp giải:

Khi rút gọn phân số có thể làm như sau:

- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.

- Chia tử số và mẫu số cho số đó.

Cứ làm như thế cho đến khi nhận được phân số tối giản.

Lời giải chi tiết:

a) \(\dfrac{6}{{10}} = \dfrac{{6:2}}{{10:2}} = \dfrac{3}{5}\)

    \(\dfrac{{96}}{{72}} = \dfrac{{96:24}}{{72:24}} = \dfrac{4}{3}\)

b) \(\dfrac{{60}}{{90}} = \dfrac{{60:30}}{{90:30}} = \dfrac{2}{3}\)

    \(\dfrac{{35}}{{25}} = \dfrac{{35:5}}{{25:5}} = \dfrac{7}{5}\)

Bài 2

Quan sát hình vẽ sau rồi tô màu đỏ vào \(\dfrac{1}{3}\) số chấm tròn, tô màu xanh vào \(\dfrac{2}{5}\) số chấm tròn, tô màu vàng vào \(\dfrac{4}{15}\) số chấm tròn.

Phương pháp giải:

- Tìm tổng số chấm tròn có trong ô vuông đã cho.

- Tìm số chấm tròn tương ứng với từng màu theo quy tắc: muốn tìm phân số của một số ta lấy số đó nhân với phân số.

Lời giải chi tiết:

Trong hình vẽ có tất cả \(90\) chấm tròn. 

\(\dfrac{1}{3}\) số chấm tròn tương ứng với \(90 \times \dfrac{1}{3} = 30\) chấm tròn.

\(\dfrac{2}{5}\) số chấm tròn tương ứng với \(90 \times \dfrac{2}{5} = 36\) chấm tròn.

\(\dfrac{4}{15}\) số chấm tròn tương ứng với \(90 \times \dfrac{4}{15} = 24\) chấm tròn. 

Vậy ta sẽ tô màu \(30\) chấm tròn màu đỏ, \(36\) chấm tròn màu xanh và \(24\) chấm tròn màu vàng.

Bài 3

Tính :

a) \(\dfrac{1}{5} + \dfrac{5}{2} =  \ldots \)                                      b) \(\dfrac{7}{4} - \dfrac{2}{8} =  \ldots \)

c) \(\dfrac{3}{5} \times \dfrac{{7}}{2} =  \ldots \)                                      d) \(\dfrac{7}{5}:\dfrac{5}{6} =  \ldots \)

Phương pháp giải:

- Muốn cộng hoặc trừ hai phân số ta quy đồng mẫu số rồi cộng hoặc trừ hai phân số sau khi quy đồng.

- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.

Lời giải chi tiết:

a) \(\dfrac{1}{5} + \dfrac{5}{} = \dfrac{2}{{10}} + \dfrac{{25}}{{10}} = \dfrac{{27}}{{10}}\)

b) \(\dfrac{7}{4} - \dfrac{2}{8} = \dfrac{{7}}{{4}} - \dfrac{1}{{4}} = \dfrac{{6}}{{4}}= \dfrac{{3}}{{2}}\)

c) \(\dfrac{3}{5} \times \dfrac{{7}}{2} = \dfrac{{3 \times 7}}{{5 \times 2}} = \dfrac{{21}}{{10}}\)

d) \(\dfrac{7}{5}:\dfrac{5}{6} = \dfrac{7}{5} \times \dfrac{6}{5}= \dfrac{{42}}{{25}}\)

Bài 4

Bé Khải chơi đàn piano trong \(\dfrac{2}{3}\) giờ, vẽ bức tranh trong \(\dfrac{3}{4}\) giờ. Hỏi bé Khải chơi đàn piano và vẽ bức tranh trong thời gian bao lâu?

Phương pháp giải:

Muốn tính thời gian bé Khải chơi đàn piano và vẽ bức tranh ta lấy thời gian bé Khải chơi đàn piano cộng với thời gian bé Khải vẽ bức tranh.

Lời giải chi tiết:

Bé Khải chơi đàn piano và vẽ bức tranh hết số thời gian là:

                   \(\dfrac{2}{3} + \dfrac{3}{4} = \dfrac{17}{12}\) (giờ)

                                   Đáp số: \(\dfrac{17}{12}\) giờ.

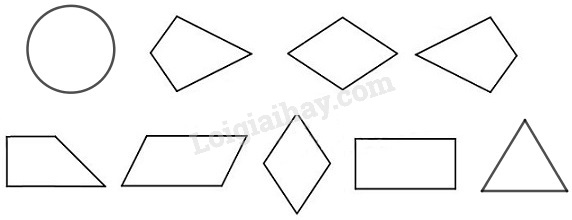
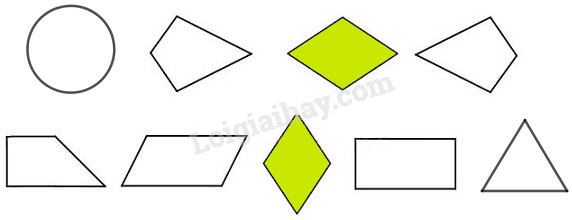
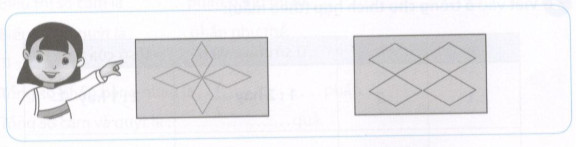
Bài 5

Tô màu vào các hình thoi: 

Phương pháp giải:

Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.

Lời giải chi tiết:

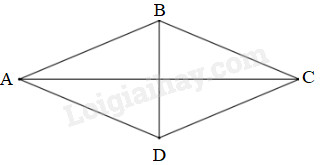
Bài 6

Viết tiếp vào chỗ chấm:

a) Hình thoi có bốn cạnh ……..

b) Hình thoi có hai đường chéo …….. với nhau và cắt nhau tại ……..

c) Hình thoi có các cặp cạnh đối diện ……..

Phương pháp giải:

Dựa vào lý thuyết về hình thoi để trả lời các câu hỏi của bài toán.

Lời giải chi tiết:

a) Hình thoi có bốn cạnh bằng nhau.

b) Hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

c) Hình thoi có các cặp cạnh đối diện song song với nhau.

Bài 7

Trong hình thoi ABCD có AC = 12cm, BD = 5cm. Tính diện tích hình thoi ABCD.

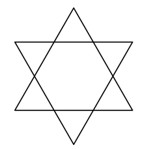
Phương pháp giải:

Hình thoi đã cho có hai đường chéo là AC và BD . Để tính diện tích hình thoi ta lấy tích độ dài hai đường chéo chia cho \(2\).

Lời giải chi tiết:

Diện tích hình thoi ABCD là:

\(\dfrac{12 \times 5}{2} = 30\;\left( {c{m^2}} \right)\)  

                Đáp số: \(30{m^2}\).

Bài 8

Tìm trong hình sau 1 hình thoi rồi tô màu vào hình thoi đó:

Phương pháp giải:

Quan sát các hình vẽ và áp dụng tính chất: hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau. 

Lời giải chi tiết:

Vui học

Tuệ Anh rất thích hình thoi, sau khi tìm hiểu nhiều mẫu trang trí có hình thoi, Tuệ Anh quyết định tự thiết kế mẫu trang trí cho mình. 

Em hãy vẽ một mẫu trang trí có hình thoi để gợi ý giúp bạn Tuệ Anh.

Phương pháp giải:

Em tự suy nghĩ và vẽ mẫu trang trí theo ý thích của mình.

Lời giải chi tiết: