Giải tuần 23: Luyện tập chung. Phép cộng phân số

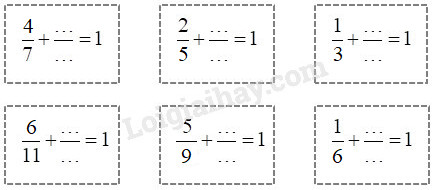
Bài 1

Khoanh vào chữ đặt trước câu trả lời đúng:

a) Phân số dưới đây bằng \(\dfrac{4}{7}\) là:

A. \(\dfrac{{12}}{{25}}\)                                           B. \(\dfrac{{20}}{{35}}\)

C. \(\dfrac{8}{{11}}\)                                           D. \(\dfrac{{16}}{{21}}\)

b) Phân số dưới đây lớn hơn 1 là:

A. \(\dfrac{{10}}{{11}}\)                                           B. \(\dfrac{{12}}{{11}}\)

C. \(\dfrac{{15}}{{15}}\)                                           D. \(\dfrac{7}{8}\)

c) Phân số lớn nhất trong các phân số dưới đây là:

A. \(\dfrac{5}{8}\)                                              B. \(\dfrac{1}{2}\)

C. \(\dfrac{6}{{11}}\)                                           D. \(\dfrac{9}{{16}}\)

Phương pháp giải:

- Áp dụng tính chất cơ bản của phân số.

- Áp dụng định nghĩa phân số lớn hơn 1: phân số có tử số lớn hơn mẫu số thì phân số đó lớn hơn 1.

- Muốn so sánh các phân số khác mẫu số ta quy đồng mẫu số các phân số rồi so sánh các phân số sau khi quy đồng.

Lời giải chi tiết:

a) Ta có: \(\dfrac{4}{7} = \dfrac{{4 \times 5}}{{7 \times 5}} = \dfrac{{20}}{{35}}\).

Các phân số \(\dfrac{{12}}{{25}};\,\,\dfrac{8}{{11}};\,\,\dfrac{{16}}{{21}}\) có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1 nên là phân số tối giản.

Vậy trong các phân số đã cho, phân số  bằng \(\dfrac{4}{7}\) là \(\dfrac{{20}}{{35}}\).

Chọn B.

b) Phân số có tử số lớn hơn mẫu số thì phân số đó lớn hơn 1.

Vậy trong các phân số đã cho, phân số lớn hơn 1 là \(\dfrac{{12}}{{11}}\).

Chọn B.

c) Chọn mẫu số chung là 176. Quy đồng mẫu số các phân số đã cho ta có:

\(\dfrac{5}{8} = \dfrac{{110}}{{176}};\)                    \(  \dfrac{1}{2} = \dfrac{{88}}{{176}}; \)

\(\dfrac{6}{{11}} = \dfrac{{96}}{{176}};\)                 \(  \dfrac{9}{{16}} = \dfrac{{99}}{{176}}.\)

Mà \(\dfrac{{88}}{{176}} < \dfrac{{96}}{{176}} < \dfrac{{99}}{{176}} < \dfrac{{110}}{{176}}\)

Do đó \(\dfrac{1}{2} < \dfrac{6}{{11}} < \dfrac{9}{{16}} < \dfrac{5}{8}\).

Vậy trong các phân số đã cho, phân số lớn nhất là \(\dfrac{5}{8}\).

Chọn A. 

Bài 2

Thay dấu * bởi chữ số thích hợp sao cho:

a) 68* chia hết cho 5 nhưng không chia hết cho 2.

b) 98* chia hết cho cả 2 và 5.

c) 82* chia hết cho cả 2 và 9.

d) 94* chia hết cho cả 3 và 5.

Phương pháp giải:

Áp dụng các dấu hiệu chia hết cho 2; 5; 9; 3:

- Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 2.

- Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5.

- Các số có chữ số tận cùng là 0 thì chia hết cho cả 2 và 5.

- Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9.

- Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3.

Lời giải chi tiết:

a) Số 68* chia hết cho 5 nên * là 0 hoặc * là 5.

Lại có số 68* không chia hết cho 2 nên * là 5.

Vậy 685 chia hết cho 5 nhưng không chia hết cho 2.

b) Để số 98* chia hết cho cả 2 và 5 thì chữ số tận cùng phải là 0, hay * là 0.

Vậy 980 chia hết cho cả 2 và 5.

c) Để số 82* chia hết cho 9 thì 8 + 2 + * chia hết cho 9, hay 10 + * chia hết cho 9. Suy ra * là 8.

Lại có số 828 chia hết cho 2.

Vậy số 828 chia hết cho cả 2 và 9.

d) Số 94* chia hết cho 5 nên * là 0 hoặc * là 5.

Số 940 có tổng các chữ số là 13. Vì 13 không chia hết cho 3 nên số 940 không chia hết cho 3.

Số 945 có tổng các chữ số là 18. Vì 18 chia hết cho 3 nên số 945 chia hết cho 3.

Vậy số 945 chia hết cho cả 3 và 5.

Bài 3

So sánh các phân số sau:

a) \(\dfrac{3}{4}\) và \(\dfrac{{13}}{{16}}\)

b) \(\dfrac{{11}}{{15}}\) và \(\dfrac{{33}}{{39}}\) 

Phương pháp giải:

a) Quy đồng mẫu số các phân số rồi so sánh các phân số sau khi quy đồng.

b) Rút gọn phân số \(\dfrac{{33}}{{39}}\) rồi so sánh với phân số \(\dfrac{{11}}{{15}}\).

Lời giải chi tiết:

a) Ta có: \(\dfrac{3}{4} = \dfrac{{3 \times 4}}{{4 \times 4}} = \dfrac{{12}}{{16}}\)

    Mà \(\dfrac{{12}}{{16}} < \dfrac{{13}}{{16}}\). Vậy \(\dfrac{3}{4} < \dfrac{{13}}{{16}}\).

b) Ta có: \(\dfrac{{33}}{{39}} = \dfrac{{33:3}}{{39:3}} = \dfrac{{11}}{{13}}\).

    Mà \(\dfrac{{11}}{{15}} < \dfrac{{11}}{{13}}\). Vậy \(\dfrac{{11}}{{15}} < \dfrac{{33}}{{39}}\).

Bài 4

Tìm hai phân số vừa lớn hơn \(\dfrac{1}{5}\) vừa bé hơn \(\dfrac{1}{2}\).

Phương pháp giải:

Cách 1 : Áp dụng cách so sánh hai phân số có cùng tử số.

Cách 2 : Quy đồng hai phân số \(\dfrac{1}{5}\) và \(\dfrac{1}{2}\) với mẫu số chung là \(10\) hoặc \(20\) hoặc \(30\), … sau đó tìm các phân số thỏa mãn điều kiện đề bài.

Lời giải chi tiết:

Cách 1 :

Ta có : \(\dfrac{1}{{5}} < \dfrac{1}{{4}} < \dfrac{1}{{3}} < \dfrac{5}{{2}}\).

Vậy ta có thể chọn hai phân số vừa lớn hơn \(\dfrac{1}{5}\) vừa bé hơn \(\dfrac{1}{2}\) là \(\dfrac{1}{{4}}\,;\,\,\dfrac{1}{{3}}\). 

Cách 2 :

Ta có: \(\dfrac{1}{5} = \dfrac{{1 \times 2}}{{5 \times 2}} = \dfrac{2}{{10}}\,\,;  \dfrac{1}{2} = \dfrac{{1 \times 5}}{{2 \times 5}} = \dfrac{5}{{10}}\).

Lại có: \(\dfrac{2}{{10}} < \dfrac{3}{{10}} < \dfrac{4}{{10}} < \dfrac{5}{{10}}\).

Vậy ta có thể chọn hai phân số vừa lớn hơn \(\dfrac{1}{5}\) vừa bé hơn \(\dfrac{1}{2}\) là \(\dfrac{3}{{10}}\,;\,\,\dfrac{4}{{10}}\) hay \(\dfrac{3}{{10}}\,;\,\,\dfrac{2}{5}\).

Lưu ý : Bài tập này có nhiều đáp số thỏa mãn yêu cầu bài toán, học sinh có thể tùy chọn các đáp số tùy ý.

Bài 5

Tính: 

a) \(\dfrac{1}{3} + \dfrac{2}{3} =  \ldots \)

b) \(\dfrac{7}{15} + \dfrac{{8}}{{15}} =  \ldots \)

Phương pháp giải:

Áp dụng quy tắc : Muốn cộng hai phân số có cùng mẫu số, ta cộng hai tử số với nhau và giữ nguyên mẫu số.

Lời giải chi tiết:

a) \(\dfrac{1}{3} + \dfrac{2}{3} = \dfrac{1+2}{{3}} = \dfrac{{3}}{{3}} = 1\)

b) \(\dfrac{7}{15} + \dfrac{{8}}{{15}} = \dfrac{{7+8}}{{15}} = \dfrac{{15}}{{15}} = 1\)

Bài 6

Rút gọn rồi tính:

a) \(\dfrac{6}{{14}} + \dfrac{5}{6} =  \ldots \)

b) \(\dfrac{8}{{12}} + \dfrac{{10}}{{22}} =  \ldots \)

Phương pháp giải:

- Rút gọn các phân số thành phân số tối giản.

- Áp dụng quy tắc : Muốn cộng hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số, rồi cộng hai phân số đó.

Lời giải chi tiết:

a) \(\dfrac{6}{{14}} + \dfrac{5}{6} = \dfrac{3}{7} + \dfrac{5}{6} = \dfrac{{18}}{{42}} + \dfrac{{35}}{{42}}\)\( = \dfrac{{53}}{{42}}\)

b) \(\dfrac{8}{{12}} + \dfrac{{10}}{{22}} = \dfrac{2}{3} + \dfrac{5}{11} = \dfrac{22}{{33}} + \dfrac{15}{{33}} \)\(= \dfrac{{37}}{{33}}\)

Bài 7

Khoanh vào chữ đặt trước câu trả lời đúng:

Một vòi nước chảy vào một bể. Giờ đầu vòi nước chảy được \(\dfrac{1}{3}\) bể, giờ thứ hai vòi chảy tiếp được \(\dfrac{1}{4}\) bể. Hỏi sau hai giờ vòi đó chảy được bao nhiêu phần của bể?

A. \(\dfrac{2}{7}\)                                                B. \(\dfrac{1}{4}\)

C. \(\dfrac{1}{3}\)                                                D. \(\dfrac{{7}}{{12}}\)

Phương pháp giải:

Muốn tính số phần nước chảy vào bể sau hai giờ ta lấy số phần nước chảy vào bể trong giờ thứ nhất cộng với số phần nước chảy vào bể trong giờ thứ hai.

Lời giải chi tiết:

Sau hai giờ vòi đó chảy được số phần của bể là:

             \(\dfrac{1}{3} + \dfrac{1}{4} = \dfrac{{7}}{{12}}\) (bể)

                                        Đáp số: \(\dfrac{{7}}{{12}}\) bể.

Chọn đáp án D.

Bài 8

Tính nhẩm rồi viết số thích hợp vào chỗ chấm:

Phương pháp giải:

Số \(1\) có thể viết thành phân số có tử số và mẫu số bằng nhau và khác \(1\).

Lời giải chi tiết:

Vui học

Viết tiếp vào chỗ chấm cho thích hợp:

Mẹ mua cho cả nhà 6 que kem như nhau, chỉ khác nhau vị của kem. Có 1 que kem vani, 2 que kem sô-cô-la, 2 que kem đậu xanh và 1 que kem dâu tây.

Phân số chỉ phần que kem vani trong tổng số các que kem mà mẹ mua là .....

Phân số chỉ phần que kem đậu xanh trong tổng số các que kem mà mẹ mua là .....

Phân số chỉ phần que kem vani và sô-cô-la trong tổng số các que kem mà mẹ mua là .....

Phương pháp giải:

Phân số chỉ phần que kem vani trong tổng số các que kem mà mẹ mua có tử số là số que kem vani và mẫu số là tổng số que kem mẹ đã mua.

Các câu khác làm tương tự như thế. 

Lời giải chi tiết:

Phân số chỉ phần que kem vani trong tổng số các que kem mà mẹ mua là \(\dfrac{1}{6}.\)

Phân số chỉ phần que kem đậu xanh trong tổng số các que kem mà mẹ mua là \(\dfrac{2}{6}.\)

Mẹ mua số que kem vani và sô-cô-la là : \(1+2 = 3\) (que kem)

Phân số chỉ phần que kem vani và sô-cô-la trong tổng số các que kem mà mẹ mua là \(\dfrac{3}{6}.\)