Giải bài tập 7.21 trang 40 SGK Toán 9 tập 2 - Cùng khám phá

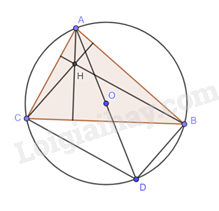
Đề bài

Cho tam giác nhọn ABC nội tiếp đường tròn (O), AD là đường kính của (O) và H là trực tâm của \(\Delta \)ABC. Chứng minh BHCD là hình bình hành.

Lời giải chi tiết

Ta có BD \( \bot \) AB do \(\widehat {ABD} = {90^o}\) (góc chắn nửa đường tròn)

CH \( \bot \) AB (CH là đường cao \(\Delta \)ABC)

Suy ra BD // CH (1)

Ta có BH \( \bot \) AC (do BH là đường cao \(\Delta \)ABC)

CD \( \bot \) AC do \(\widehat {ACD} = {90^o}\) (góc chắn nửa đường tròn)

Suy ra BH // CD (2)

Từ (1) và (2) suy ra tứ giác BHDC là hình bình hành.