Giải bài tập 5.36 trang 127 SGK Toán 9 tập 1 - Cùng khám pháCho hai đường tròn tâm O và I cắt nhau tại M và N. Vẽ một đường thẳng qua M cắt (O) tại A và cắt (I) tại B, một đường thẳng qua N cắt (O) tại C và (I) tại D. Chứng minh rằng AC//BD. Quảng cáo
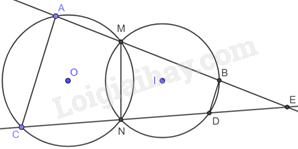
Đề bài Cho hai đường tròn tâm O và I cắt nhau tại M và N. Vẽ một đường thẳng qua M cắt (O) tại A và cắt (I) tại B, một đường thẳng qua N cắt (O) tại C và (I) tại D. Chứng minh rằng AC//BD. Phương pháp giải - Xem chi tiết + Chứng minh \(\widehat {NMB} + \widehat {NDB}\)$=\frac{1}{2}\left( sđ\overset\frown{NDB}+sđ\overset\frown{NMB} \right)$\( = \frac{1}{2}{.360^o}\)\( = {180^o}\). + Chứng minh \(\widehat {ACN} + \widehat {AMN} = {180^o}\), \(\widehat {NMB} + \widehat {AMN} = {180^o}\) nên \(\widehat {ACN} = \widehat {NMB}\) + Do đó, \(\widehat {ACN} + \widehat {NDB} = {180^o}\). + Gọi E là giao điểm của AB và CD. Do đó: \(\widehat {BDE} + \widehat {NDB} = {180^o}\). Suy ra \(\widehat {ACN} = \widehat {BDE}\) nên AC//BD. Lời giải chi tiết
Xét (I): Vì NMB là góc nội tiếp chắn cung NDB nên $\widehat{NMB}=\frac{1}{2}sđ\overset\frown{NDB}$. Vì NDB là góc nội tiếp chắn cung NMB nên $\widehat{NDB}=\frac{1}{2}sđ\overset\frown{NMB}$. Do đó, \(\widehat {NMB} + \widehat {NDB}\)$=\frac{1}{2}\left( sđ\overset\frown{NDB}+sđ\overset\frown{NMB} \right)$\( = \frac{1}{2}{.360^o}\)\( = {180^o}\)(1) Chứng minh tương tự ta có: \(\widehat {ACN} + \widehat {AMN} = {180^o}\). Mà \(\widehat {NMB} + \widehat {AMN} = {180^o}\) nên \(\widehat {ACN} = \widehat {NMB}\) (2) Từ (1) và (2) ta có: \(\widehat {ACN} + \widehat {NDB} = {180^o}\). Gọi E là giao điểm của AB và CD. Do đó: \(\widehat {BDE} + \widehat {NDB} = {180^o}\) Suy ra \(\widehat {ACN} = \widehat {BDE}\), mà hai góc này ở vị trí đồng vị. Do đó, AC//BD.  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
